Составление уравнений для переходного режима
При расчетах и проектировании САУ широко используется преобразование Лапласа, которое позволяет заменить дифференциальные уравнения алгебраическими. Преобразование Лапласа определяется соотношением
 ,
,
где 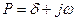 − комплексная величина, а
− комплексная величина, а 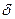 и
и 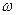 - вещественные числа.
- вещественные числа.
Преобразование кратко записывают в виде 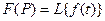 . Здесь
. Здесь 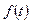 называется оригиналом, а
называется оригиналом, а 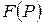 – изображением функции
– изображением функции 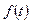 . Рассмотрим некоторые свойства и правила преобразования Лапласа:
. Рассмотрим некоторые свойства и правила преобразования Лапласа:
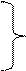
1. 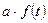
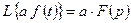
– свойство линейности.
2. 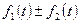
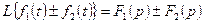
3. 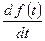
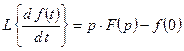 – правило дифференцирования.
– правило дифференцирования.
4. 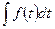
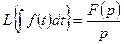 – правило интегрирования.
– правило интегрирования.
5. 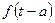
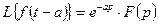 – теорема запаздывания.
– теорема запаздывания.
Обычно САУ рассчитываются при нулевых начальных условиях, т.е. входной сигнал прикладывается к системе после установившего режима. Поэтому все члены, зависящие от начальных условий, будут равны нулю.
Рассмотрим нахождение преобразования Лапласа линейного дифференциального уравнения второго порядка.
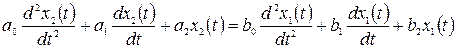 . (1.1)
. (1.1)
Умножим левую и правую части уравнения (1.1) на 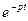 и проинтегрируем от
и проинтегрируем от 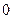 до
до 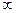 .
.
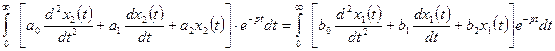 .
.
Используя сокращенную форму записи, получим:
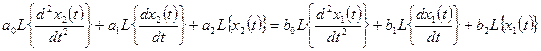 .
.
Используя свойство линейности и правило дифференцирования при нулевых начальных условиях, получим:
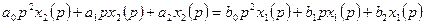 . (1.2)
. (1.2)
Сравнивая уравнения (1.1) и (1.2), можно заметить, что формально уравнение (1.2) можно получить из уравнения (1.1), если в нем заменить 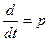 , где
, где 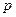 − оператор дифференцирования.
− оператор дифференцирования.
Так как уравнение (1.2) является алгебраическим, то из него найдем отношение:
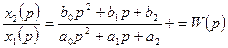
где 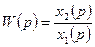 − передаточная функция.
− передаточная функция.
Итак, передаточной функцией называется отношение преобразования по Лапласу выходного сигнала к преобразованию по Лапласу входного сигнала при нулевых начальных условиях.
Для линейной системы 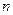 -ого порядка передаточная функция будет равна:
-ого порядка передаточная функция будет равна:
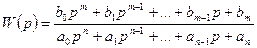 .
.
 2014-02-09
2014-02-09 440
440








