Пусть дан на прямоугольной области сетчатый каркас поверхности.
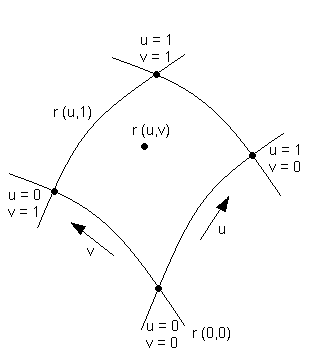 |
Сетка кривых разбивает поверхность на совокупность ячеек, каждая из которых ограничена, параметрически представлена парой u – кривых и v – кривых.
Заданная ячейка поверхности находится в пределах:
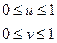
и представляет собой исходную часть поверхности, ограниченную четырьмя исходными границами. Форрест предложил наглядную трактовку поверхности Кунса.
Данный алгоритм состоит в следующем:
Для задания ячейки поверхности решается в начале более простая задача (одна из пар кривых является линейчатой).
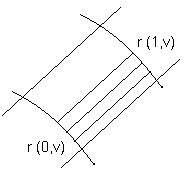 |
Тогда для этой поверхности функция имеет вид:
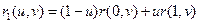
Аналогично построим для этого же элемента линейчатости поверхность, ограниченную параметрами.
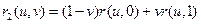
Сумма r1 и r2 дает новую поверхность у которой граничные кривые будут являться уравнениями кривой и прямого отрезка.
Для восстановления начальных исходных граничных кривых необходимо из уравнения 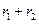 вычесть скалярную линейную поверхность, границами которой служат эти прямолинейные отрезки.
вычесть скалярную линейную поверхность, границами которой служат эти прямолинейные отрезки.
Тогда результирующая поверхность определяется как:
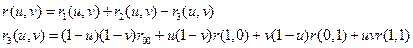
 2014-02-09
2014-02-09 1259
1259








