Дисконтирование во времени

Ранее была получена формула:

,

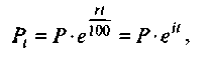которая позволяет определить величину вклада Р_t через проме­жуток времени t, если начальный вклад составляет Р и процент­ная ставка r, или 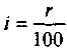исчисляется непрерывно.

Рассмотрим теперь обратную задачу для нахождения стоимо­сти аннуитета (регулярных платежей) применительно к непрерыв­ным процентам.

В этом случае платежи зависят от времени, т.е. являются фун­кцией от t, что можно записать как Р =P(t) по­требуется определить величину вклада Р через Т лет. Для ре­шения разобьем Т лет на n равных промежутков времени Δt, как показано на рис. 4.13.

Если поступления непрерывны, то в течение малого промежут­ка времени Δt их можно считать постоянными, а их величина от момента времени t_i, до t_i+1 составит приближенно

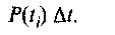
За время (Т- t_i) наращенная сумма, рассчитанная по формуле непрерывных процентов, за счет начисления процентов на взнос P(t_i)Δt станет равной

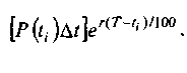
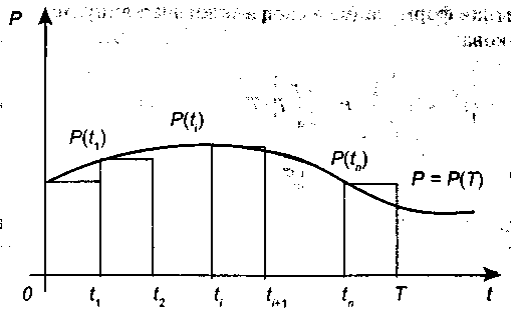
Теперь, чтобы получить общую величину вклада S через T лет, достаточно сложить все «малые вклады», а именно

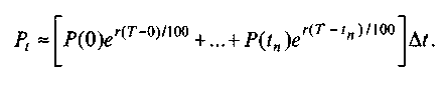
Это приближенное равенство станет точным, если промежу­ток времени Δt будет становиться сколь угодно малым. В этом случае сумма, стоящая в правой части, превращается в опреде­ленный интеграл.

Окончательная формула имеет вид:

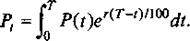
(4.4.9)

Ранее рассматривалось понятие дисконта, связанное для не­прерывных процентов с формулой

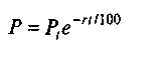(4.4.10)

Эта формула дает возможность определить величину началь­ного вклада Р, если известно, что через t лет он должен составить величину Р_t, а непрерывная процентная ставка равна r. Задача аннуитета в этом случае может быть сформулирована так: найти величину начального вклада Р, если регулярные выплаты по это­му вкладу должны составлять Р_t ежегодно в течение Т лет.

Расчетная формула (ее вывод аналогичен аннуитету с плате­жами) такова:

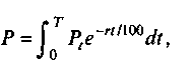(4.4.11)

где r — непрерывная процентная ставка.

Для примера вычислим начальный вклад Р, если выплаты должны составлять 100 у.е. в течение 4 лет, а процентная ставка рав­на 7, т.е.

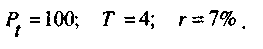
Подставляя численные значения в формулу, получаем:

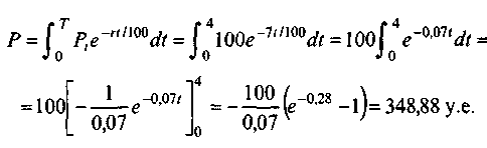
Это и есть искомый начальный вклад.

Пусть поступающий ежегодно доход изменяется во времени и описывается функцией P_t(t)= f(t) и при удельной норме процент­ной ставки, равной i, процент начисляется непрерывно. Как и в предыдущем пункте можно показать, что в этом случае дисконти­рованный доход Р за время Т вычисляется по формуле

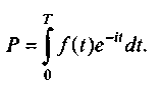. (4.4.12)

Пример 4.22. Определим дисконтированную сумму Р при f(t) = S₀(1 + kt), где S₀ — начальные капиталовложения, k — еже­годная доля их увеличения. Иными словами, при заданных величинах i и k требуется оценить, что выгоднее: наращивать ка­питаловложения или вложить их одновременно при непрерывно начисляемой процентной ставке.

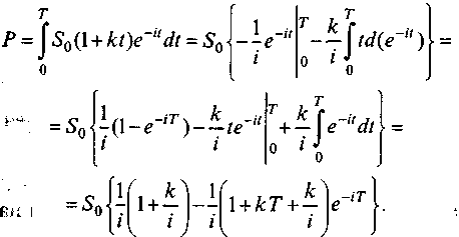
Из полученной формулы можно сделать некоторые выводы:

1.Чем выше процентная ставка i, тем меньше дисконтная сум­ма Р и, следовательно, выше доход, вычисляемый как разность между суммой ежегодно растущих капиталовложений за Т лет и величиной Р. Если рассматривать Р как дисконтный доход, то увеличение процентной ставки i снижает рентабельность помеще­ния капитала.

2.Увеличение интенсивности ежегодных капиталовложений (k) приводит к увеличению Р.

3.При неизменных i и k дисконтный доход растет с увеличе­нием промежутка времени Т (количества лет).

Например, при процентной ставке r = 5% (i = 0,05) и при еже­годном увеличении капиталовложений на 5% (k = 0,05) получаем, что за 5 лет дисконтная сумма Р = 5S₀, в то время как сумма еже­годных капиталовложений за этот период составит Р_е = 6,25 S₀ при k = 0,1 (10%-ное увеличение ежегодных капиталовложений) и тех же самых i и Т соответственно имеет Р = 5,5 S₀ и Р_е = 6,5 S₀, т.е. в первом случае разность Р_е — P_i = 1,25 S₀, тогда как во втором случае она снижается до = S₀.

При аналогичных оценочных расчетах в реальных условиях следует учитывать существенную роль темпа инфляции, который, в первую очередь, определяет приемлемую величину промежутка времени Т. Очевидно, что при высоком уровне инфляции выгод­ны только краткосрочные капиталовложения, которые гаранти­руют минимальные значения риска.

Пример 4.23. Определить дисконтируемый доход за три года при процентной ставке 8%, если первоначальные капиталовложения составили 1 млн у.е., и намечается ежегодно увеличивать ка­питаловложения на 0,1 млн у.е.

Решение. Ясно, что капиталовложения задаются функцией f(t) = 1 + 0,1 t. По формуле (4..4.12) записываем дисконтирован­ную сумму капиталовложений:

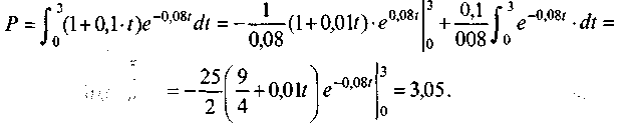
Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 1 до 1,3 млн у.е. равносильны одновременным первоначальным вло­жениям 3,05 млн у.е. при той же, начисляемой непрерывно, про­центной ставке.

Пример 4.24. Под строительство завода задан непрерывный денежный поток со скоростью f(t) = -t² + 20t + 5 (млн у.е.) в тече­ние 8 лет с годовой процентной ставкой, равной 5%. Найти дис­контированную стоимость этого потока.

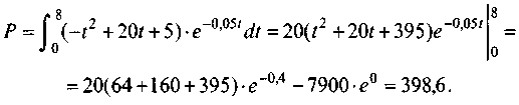
Дважды провели интегрирование по частям.

Таким образом, начальная сумма капиталовложений равня­лась бы 398,6 млн у.е.

Рассмотрим теперь задачу нахождения капитала (основных фондов) по известным чистым инвестициям. Напомним: чистые инвестиции (капиталовложения) — это общие инвестиции, про­изводимые в экономике в течение определенного промежутка вре­мени (чаще всего — года), за вычетом инвестиций на возмещение выходящих из строя основных фондов (капитала). Таким обра­зом, за единицу времени капитал увеличивается на величину чис­тых инвестиций.

Если капитал обозначить как функцию времени K(t), а чистые инвестиции — I(t), сказанное выше можно записать в виде:

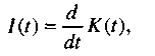
т.е. это производная от капитала по времени t.

Часто требуется найти приращение капитала за период с мо­мента времени t₁ до t₂, т.е. величину

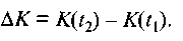
Замечая, что K(t) является первообразной для функции I(t), и вспоминая формулу, связывающую первообразную с определен­ным интегралом, можно сразу написать:

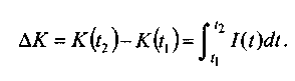
Пусть, например, по заданным чистым инвестициям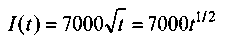

нужно определить приращение капитала за три года. Очевидно, что t₁= 0,

t₂ = 3.

Непосредственное применение формулы дает:

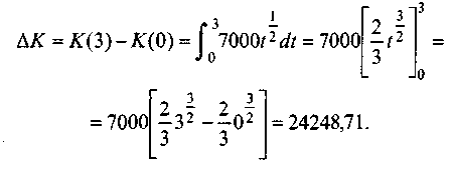
Теперь, оставляя неизменной функцию I(t), задающую инвес­тиции, попробуем ответить на вопрос: через сколько лет прира­щение составит 50000, т.е.

ΔК= 50000.

Обозначая искомый промежуток времени через Т, можно на­писать

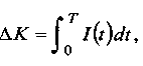
или, подставляя численные значения,

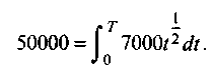
Мы получили уравнение, которое интересно тем, что неизвес­тная величина Т — это верхний предел интегрирования. Для ре­шения вычислим определенный интеграл

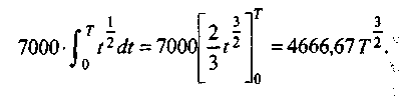
Теперь уравнение можно записать в виде:

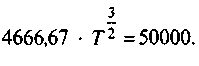
В данном случае это нелинейное уравнение решается достаточно просто. Разделим обе части на постоянный множитель, что дает:

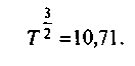
Возводя обе части в степень 2/3

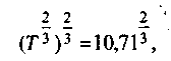
окончательно получаем

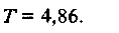
Именно столько лет требуется, чтобы приращение капитала составило 50000.