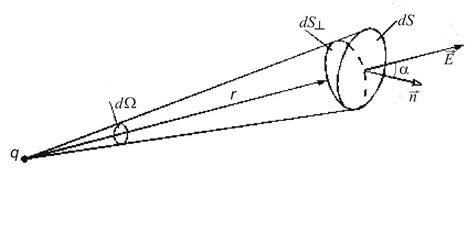
Рассмотрим элементарную площадку 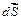 , находящуюся в поле, созданном точечным источником q, расположенным в точке наблюдения. Вектор нормали к площадке
, находящуюся в поле, созданном точечным источником q, расположенным в точке наблюдения. Вектор нормали к площадке 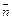 не совпадает с вектором напряженности поля в этой точке,
не совпадает с вектором напряженности поля в этой точке, 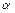 - угол между вектором нормали к поверхности и вектором напряженности поля; r – расстояние от источника поля до площадки. Рассмотрим площадку
- угол между вектором нормали к поверхности и вектором напряженности поля; r – расстояние от источника поля до площадки. Рассмотрим площадку 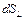 , элементы которой перпендикулярны r. Найдем поток через площадку
, элементы которой перпендикулярны r. Найдем поток через площадку 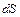 :
:
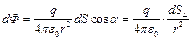
Введем понятие телесного угла:
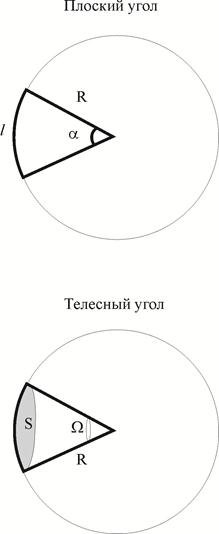
Количественной мерой плоского угла является отношение длины дуги l к ее радиусу R. При этом центр кривизны находится в вершине угла.
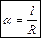
Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы.
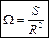
Таким образом, в наших обозначениях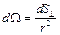 - телесный угол.
- телесный угол.
Это пространственный угол, под которым из точки расположения точечного
заряда видна площадка 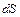 (или
(или 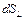 - они видны под одним и тем же углом).
- они видны под одним и тем же углом).
Тогда выражение для элементарного потока принимает вид:
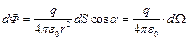
Угол 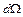 положителен, если площадка
положителен, если площадка 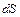 обращена к заряду внутренней стороной, и отрицателен, если внешней.
обращена к заряду внутренней стороной, и отрицателен, если внешней.
Рассмотрим 2 случая.
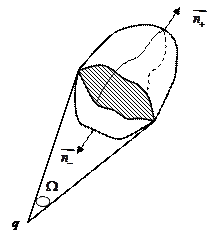
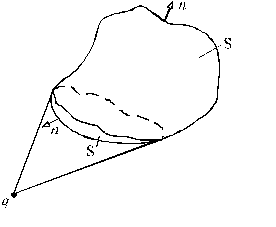
1) 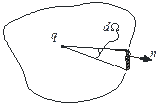 Пусть заряд q расположен внутри некоторой замкнутой поверхности (контур, изображенный на рисунке, - след от пересечения нашей поверхности с плоскостью листа). Мы будем пользоваться понятием внешней нормали
Пусть заряд q расположен внутри некоторой замкнутой поверхности (контур, изображенный на рисунке, - след от пересечения нашей поверхности с плоскостью листа). Мы будем пользоваться понятием внешней нормали 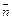 , которая направлена из части пространства, охватываемой поверхностью, наружу. Мы рассматриваем как раз тот случай, когда элементарная площадка обращена к заряду внутренней стороной, т.е. угол
, которая направлена из части пространства, охватываемой поверхностью, наружу. Мы рассматриваем как раз тот случай, когда элементарная площадка обращена к заряду внутренней стороной, т.е. угол 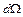 – положительное число. Найдем поток вектора напряженности через нашу поверхность. Так как поток – величина аддитивная, полный поток равен сумме элементарных потоков:
– положительное число. Найдем поток вектора напряженности через нашу поверхность. Так как поток – величина аддитивная, полный поток равен сумме элементарных потоков:
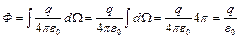
 Полный телесный угол =
Полный телесный угол = 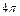 . Для того чтобы в этом убедиться, представим, что в точке расположения заряда находится сфера (на рисунке, на правом экране, она–розовая, радиусом
. Для того чтобы в этом убедиться, представим, что в точке расположения заряда находится сфера (на рисунке, на правом экране, она–розовая, радиусом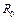 )и запишем отношение полной поверхности сферы
)и запишем отношение полной поверхности сферы 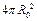 к квадрату ее радиуса
к квадрату ее радиуса 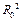 . Получим как раз
. Получим как раз 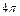 .
.
Итак, мы получили, что в случае, когда заряд находится внутри замкнутой поверхности, поток поля этого заряда через поверхность
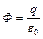
2) Теперь рассмотрим случай, когда заряд находится вне рассматриваемой замкнутой поверхности. Из точки наблюдения, в которой расположен заряд, поверхность видна под телесным углом 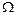 . На рисунке верхней части поверхности соответствует внешняя нормаль
. На рисунке верхней части поверхности соответствует внешняя нормаль 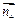 , и телесный угол, соответствующий этой части поверхности, будет иметь знак «+». Нижней же части поверхности
, и телесный угол, соответствующий этой части поверхности, будет иметь знак «+». Нижней же части поверхности
соответствует внешняя нормаль 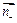 , телесный угол, соответствующий этой части поверхности, будет иметь знак «-». Тогда полный поток, пронизывающий нашу поверхность, может быть представлен в виде суммы двух потоков:
, телесный угол, соответствующий этой части поверхности, будет иметь знак «-». Тогда полный поток, пронизывающий нашу поверхность, может быть представлен в виде суммы двух потоков: 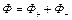 , где
, где 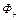 - поток через верхнюю часть поверхности,
- поток через верхнюю часть поверхности, 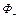 - поток через нижнюю часть нашей поверхности. Распишем это выражение, учитывая, что поверхность со знаком «+» и поверхность со знаком «-» опираются на телесные углы равные по величине, но противоположные по знаку:
- поток через нижнюю часть нашей поверхности. Распишем это выражение, учитывая, что поверхность со знаком «+» и поверхность со знаком «-» опираются на телесные углы равные по величине, но противоположные по знаку:
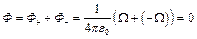
Т.е. получаем, что в случае, когда заряд находится вне замкнутой поверхности, поток этого заряда через поверхность = 0.
Мы рассмотрели только случай, когда поле создается единственным точечным зарядом. Если же поле создается системой точечных зарядов, то поток поля 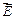 , проинтегрированный по всей замкнутой поверхности, в силу принципа суперпозиции может быть представлен в виде:
, проинтегрированный по всей замкнутой поверхности, в силу принципа суперпозиции может быть представлен в виде:
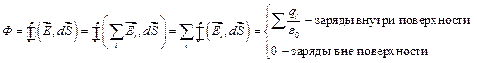
 2014-02-09
2014-02-09 569
569








