Локальная (дифференциальная) форма теоремы Гаусса

Рассмотрим небольшой заряд dq, распределенный в объеме dV с плотностью 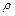. В соответствие с теоремой Гаусса, поток 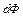вектора 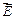через элементарную замкнутую поверхность, охватывающую объём 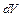, находится по формуле .

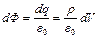Из полученного выражения видно, что ,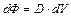

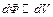
Здесь D характеризует плотность пространственного распределения источников поля.

D – дивергенция (расходимость) векторного поля: 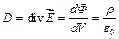. Если представить силовые линии, создаваемые, например, точечным источником поля, то видно, что они от него расходятся (или к нему сходятся). Тогда теорема Гаусса принимает следующий вид (в дифференциальной форме):

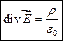- дифференциальная форма теоремы Гаусса.