Уравнения Пуассона (1812 г) и Лапласа (1782 г).
Теорема Гаусса в дифференциальной форме 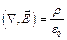 и дифференциальное соотношение
и дифференциальное соотношение 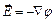 позволяют получить следующее:
позволяют получить следующее: 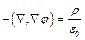
 - уравнение Пуассона, где
- уравнение Пуассона, где  - лапласиан или оператор Лапласа.
- лапласиан или оператор Лапласа.
Если между проводниками нет зарядов, т.е. 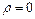 , то уравнение Пуассона переходит в более простое
, то уравнение Пуассона переходит в более простое и называется - уравнением Лапласа.
и называется - уравнением Лапласа.
Решения уравнений Пуассона и Лапласа единственны при данных граничных условиях.
Пример. (Иродов 3.49) В некоторой области пространства потенциал зависит только от координаты x как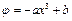 . Найти распределение объемного заряда
. Найти распределение объемного заряда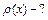
 , отсюда
, отсюда 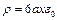 .
.
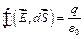
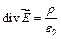

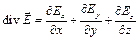
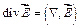



 2014-02-09
2014-02-09 528
528







