Мощность континуума

Несчётные множества.

Теорема 1.14. Множество всех вещественных чисел отрезка 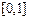несчётно.

Доказательство. Предположим противное, то есть что множество 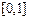счётное и 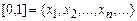. Разобьём отрезок 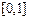на три равные части и возьмём тот из них, который не содержит . Если отрезков не содержащих два, то берём любой из них. Обозначим его 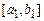. Разбиваем теперь отрезок 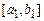на три равные части берём тот, который не содержит 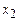и так далее. По построению 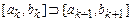. Следовательно, по теореме о вложенных отрезках (принцип Кантора), существует точка 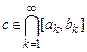. Полученное противоречие доказывает теорему.

Определение. Будем говорить,что множство 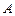имеет мощность континуума (мощность С), если оно эквивалентно отрезку .

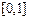Задачи для самостоятельного решения.

Доказать, что множества 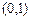, , 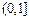, 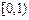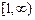имеют мощность континуума.

Теорема 1.15. Конечное или счётное объединение множеств мощности континуум имеет мощность конинуума.

Доказательство. Пусть каждое 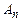имеет мощность континуума. Тогда 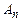имеет ту же мощность, что и полуинтервал 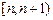. Тогда, по теореме склеивания, множество 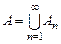имеет ту же мощность, что и множество .

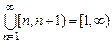Теорема 1.16. Множество иррациональных чисел имеет мощность континуума.

Доказательство. Так как множество 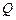рациональных чисел счётно, то множество иррациональных чисел 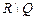имеет ту же мощность, что и множество вещественных чисел 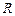, то есть мощность континуума. Теорема доказана.