Сравнение мощностей

Выше мы рассмотрели множества различной мощности. Будем обозначать мощность множества 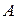либо значком 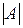, либо значком 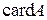. Возникает вопрос о сравнении множеств по их мощности. Для множеств содержащих конечное число элементов естественно считать, что если множества содержат одинаковое число элементов, то их мощности равны, то есть множества эквивалентны, и писать в этом случае 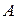~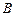. В случае равенства мощностей множеств 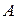и 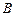будем писать 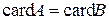. Если множество 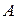содержит меньше элементов, чем множество 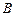, то в случае конечных множеств 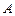~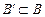и тогда будем писать 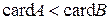. По аналогии Если множество 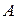содержит больше элементов, чем множество 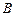, то в случае конечных множеств 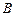~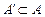и тогда будем писать .

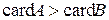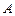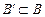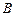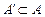Для бесконечных множеств возможно такое же сравнение с учётом того, что если ~и ~, то 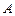~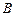. Будем в этом случае писать 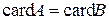. Есл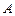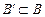и ~и 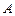не эквивалентно 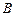, то будем писать, что .

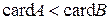Мощность счётного множества обозначается через.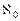

Множество мощности континуума будем обозначать .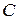

Множество всех подмножеств множества 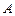имеет мощность 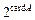. Возникает вопрос о равенстве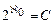, то есть вопрос о том имеется ли мощность промежуточная между мощностью счётного множества и мощностью континуума. В этом вопросе заключается гипотеза континуума.

Пример. Рассмотрим множество вещественных функций, заданных на отрезке 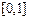. Предположим, что это множество имеет мощность континуума, следовательно, существует биекция его на отрезок 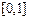. Эта биекция ставит в соответствие каждой функции 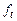точку 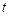из отрезка 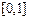. Определим функцию соотношением 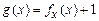. Тогда для всякого 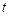при 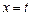имеем 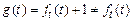. То есть мы нашли функцию, которой не соответсвует ни одна точка отрезка 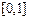. Следовательно, множество вещественных функций заданных на отрезке 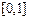имеет мощность большую мощности континуума.