2014-02-09
1015
В основе различных методов преобразования электрических схем лежит понятие эквивалентности, согласно которому напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными.
Преобразования электрических схем применяются для упрощения расчетов.
Рассмотрим наиболее типичные методы преобразования.
Последовательное соединение элементов.
При последовательном соединении элементов через них протекает один и тот же ток I (рис.1.18). Согласно второму закону Кирхгофа, напряжение, приложенное ко всей цепи
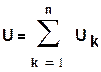(1.27)
Для последовательного соединения сопротивлений r1,r2...rn (рис. 1.18) с учетом (1.6) будем иметь
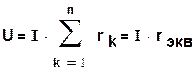
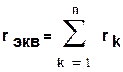(1.28)
Ток в цепи с последовательным соединением элементов равен:
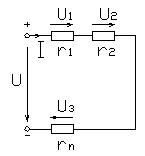
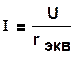(1.29)
а напряжение на n-ом элементе равно
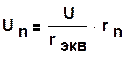(1.30)
При последовательном соединении источников напряжения они заменяются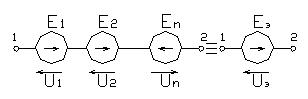 
одним эквивалентным источником с напряжением Uэкв, равным алгебраической сумме напряжений отдельных источников.
Рис 1.19 Причем со знаком «+» берутся напряжения, совпадающие с напряжением эквивалентного источника, а со знаком «-» - несовпадающие (рис.1.19).
|
|
|
Параллельное соединение элементов.
Соединение групп элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным (рис.1.20). Согласно первому Кирхгофа, ток всей цепи I равен алгебраической сумме токов в параллельных ветвях, т.е.
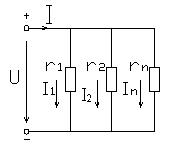
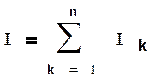(1.31)
На основании этого уравнения с учетом (1.8) для параллельного соединения резистивных элементов получаем:
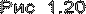
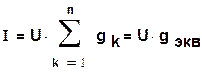
где -эквивалентная проводимость. (1.32)
Токи и мощности параллельно соединенных ветвей при U =const (рис. 1.20) не зависят друг от друга и определяются по формулам:
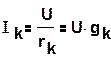
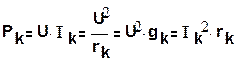(1.33)
Мощность всей цепи равна:
, 
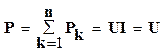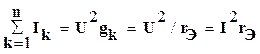(1.34)
где rэ=1/gэ -эквивалентное сопротивление цепи.
При увеличении числа параллельных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р. Токи и мощности ранее включенных ветвей не изменяются.
Рассмотрим частные случаи параллельного соединения резистивных элементов.
а) параллельное соединение двух элементов
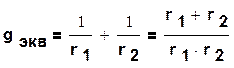
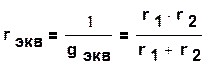(1.35)
б) параллельное соединение n ветвей с одинаковыми сопротивлениями
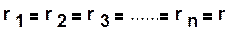
(1.36)
Эквивалентное преобразование резистивноготреугольника в звезду.
Под соединением треугольником (рис.1.21.а) понимается такое, при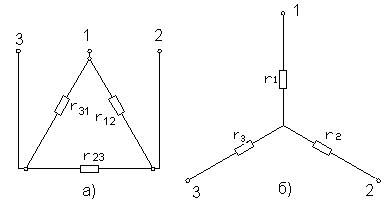 
котором конец одного элемента соединяется с началом второго, конец второго- с началом третьего, а конец третьего - с началом первого. Узловые точки 1,2,3 подключаются к остальной
Рис 1.21 части электрической цепи. Соединение звездой получается при объединении начал или концов сопротивлений в одну точку (рис.1.21.б).
|
|
|
При расчете электрических цепей оказывается полезно преобразовать треугольник в звезду или совершить преобразование звезды в треугольник.
Замена треугольника эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками 1 и 2, 2 и 3,3 и 1 остались без изменения.
С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:
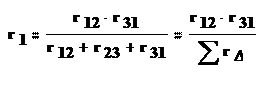
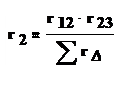
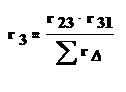(1.37)
При замене резистивных элементов, соединенных звездой, эквивалентным треугольником, пользуются следующими формулами
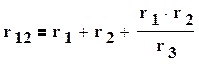
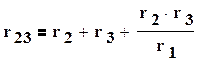(1.38)
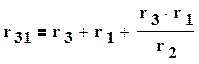
1.8.3. Метод контурных токов .
Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом расчета по законам Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так Рис 1.22 называемые контурные токи,
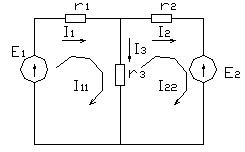
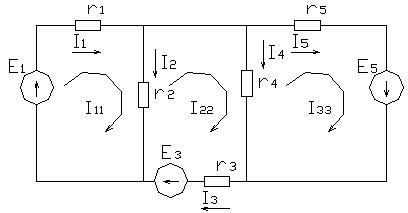
замыкающиеся в контурах. На рис.1.22. в виде примера показана двухконтурная цепь, в которой I11 и I22 - контурные токи. Токи в сопротивлениях r1 и r2 равны соответствующим контурным токам; ток в сопротивлении r3 являющемся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви r3 встречно.
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q +1 уравнений. Так, в схеме рис.1.22 q = 2 p = 3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис.1.22., где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис.1.22) могут быть записаны два уравнения по второму закону Кирхгофа, а
именно:
, 
,
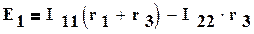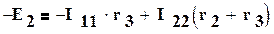здесь (r1 + r3) и (r2 + r3) - собственные сопротивления контуров 1 и 2, r3 -
общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.
I1 = I11; I2 = I22; I3 = I11 - I22.
