2014-02-09
515
Определение 1. Если каждому значению некоторой переменной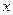 
,принадлежащему области М, соответствует одно определенное значение другой переменной 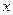, то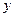 
– есть функция от 
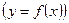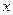. - область определения, 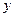- множество значений функции.
Определение 2. Пусть каждому натуральному числу n поставлено в соответствие некоторое число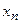 
. Совокупность элементов 
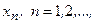называется числовой последовательностью или последовательностью.
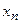- элемент последовательности, 
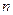-номер элемента.
Обозначение: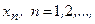 
или 
.
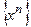Последовательность является функцией, определенной на множестве натуральных чисел и принимающей значения на множестве действительных чисел.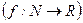 
Пример: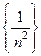 
обозначает последовательность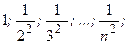 
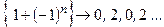
Определение 3. Последовательность 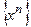называется ограниченной сверху (снизу), если существует вещественное число 
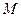(число 
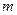) такое, что каждый элемент последовательности 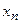удовлетворяет неравенству:
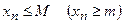
Определение 4. Последовательность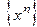 
называется ограниченной с обеих сторон (или просто ограниченной), если она ограничена и сверху и снизу, то есть
|
|
|
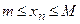
Определение 5 Последовательность называется ограниченной тогда и только тогда, когда существует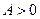 
, для любого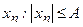 
Способы задания последовательности:
1. Общая формула: задается общий член последовательности
пример: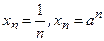 
и т.д.
2. Рекуррентная формула (от латинского recurrens- возвращающийся):
а)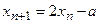 
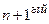элемент выражается через предыдущие:
б)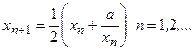 
3. Описательный:
а) 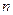-ый член последовательности = 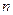-му приближению числа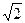 
б)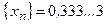 
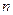(раз)
