Предел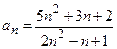

Пример. (разделим числитель и знаменатель на )

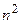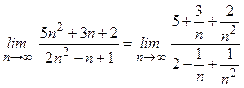
Все последовательности сходящиеся

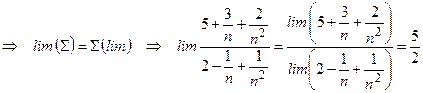
Теорема 6. Сохранение знака.

Если все элементы сходящейся последовательности 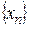, по крайней мере, с некоторого номера, удовлетворяют неравенству 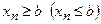, то и предел этой последовательности удовлетворяет тому же неравенству. (Доказывается методом от противного)

Пусть выполняется: 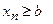начиная с 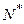, но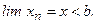

Тогда по определению сходящейся последовательности для 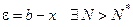, что 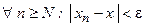или 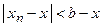, или же

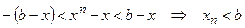
(противоречит условию теоремы).

Замечание. Если все элементы последовательности 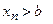, то отсюда не следует строгое неравенство для предела, т.е. все равно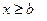

Пример. 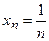, то есть 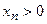, но 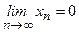, т.е. не удовлетворяет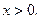

Теорема 7. Принцип двустороннего ограничения.

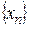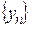Пусть и - сходящиеся последовательности, .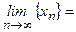

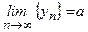Пусть 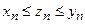(*), начиная с 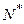. Тогда: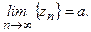

Доказательство.

Пусть неравенства справедливы, начиная с некоторого 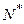, тогда начиная с того же номера 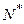справедливы и неравенства:

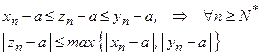
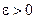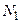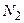Зафиксируем , тогда существуют и , что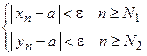

Обозначим через 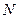наибольшее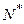, , 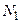, 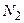тогда при 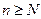будут справедливы оба неравенства и, следовательно, 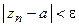, т.е.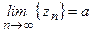

Теорема 8 Признак существования предела.

Если последовательность возрастает и ограничена, то она сходится (т.е. имеет предел) (без доказательства). Аналогично и для убывающей последовательности.

Иначе: Если последовательность монотонна и ограничена, она имеет предел.