Теорема 1: ∑ сходящихся последовательностей 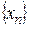 и
и 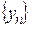 есть сходящаяся последовательность, предел которой равен ∑ пределов последователей
есть сходящаяся последовательность, предел которой равен ∑ пределов последователей 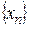 и
и 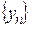
Доказательство.
Пусть 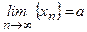 ,
, 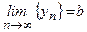
 (специальное представление)
(специальное представление)
где 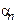 и
и 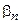 - элементы бесконечно-малых последовательностей.
- элементы бесконечно-малых последовательностей.
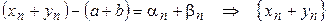 - сходится к
- сходится к 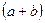
Теорема 2. Разность сходящихся последовательностей равна сходящейся последовательности, предел которой равен разности пределов.
Теорема 3 Произведение сходящихся последовательностей 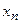 и
и 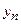 равно сходящейся последовательности, предел которой равен произведению пределов
равно сходящейся последовательности, предел которой равен произведению пределов 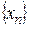 и
и 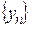 .
.
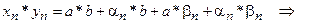
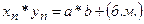
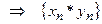 сходится к
сходится к 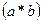
Следствие. Постоянный множитель можно выносить за знак предела т.к. 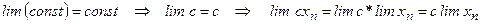
Теорема 4. Частное двух сходящихся последовательностей 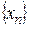 и
и 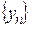 (предел второй не равен 0) определено, начиная с некоторого номера и равно сходящейся последовательности, предел которой равен частному пределов
(предел второй не равен 0) определено, начиная с некоторого номера и равно сходящейся последовательности, предел которой равен частному пределов 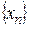 и
и 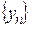 .
.
Доказательство.
Пусть 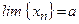 ,
, 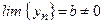
Начиная с некоторого 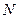 , элементы
, элементы 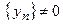 , можно рассматривать частное
, можно рассматривать частное 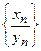
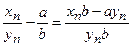
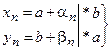
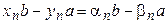
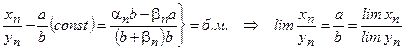
Теорема 5. Всякая сходящаяся последовательность ограничена. Если сходящаяся последовательность имеет предел, следовательно, она ограниченна.
Доказательство.
Пусть 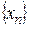 - сходящаяся последовательность,
- сходящаяся последовательность, 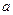 - её предел. Зафиксируем
- её предел. Зафиксируем 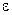 и найдём такой
и найдём такой 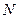 , что
, что 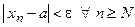 или, что тоже самое,
или, что тоже самое,
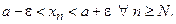 Обозначим через
Обозначим через  наибольшее из чисел:
наибольшее из чисел: 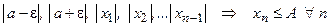 , т.е. ограниченная.
, т.е. ограниченная.
Замечание. Обратное не всегда выполняется 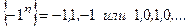 ограниченная, но не сходящаяся.
ограниченная, но не сходящаяся.
 2014-02-09
2014-02-09 500
500








