Бесконечно малые последовательности
Определение. Последовательность 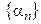 называется бесконечно малой, если
называется бесконечно малой, если 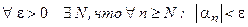
Пример. 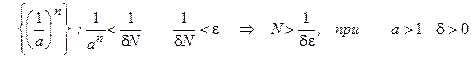

1) 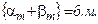 если
если 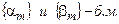
Доказательство:
Пусть 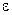 – фиксирована, т.к.
– фиксирована, т.к.
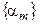 - бесконечно-малая последовательность
- бесконечно-малая последовательность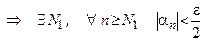 (1)
(1)
Аналогично,
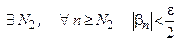 (2)
(2)
Пусть 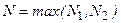 , следовательно,
, следовательно, 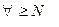 выполняется (1) и (2)
выполняется (1) и (2)
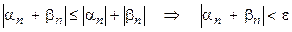
2) Если 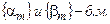 , следовательно
, следовательно 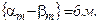
Следствие. ∑ любого числа бесконечно-малых последовательностей есть бесконечно-малая последовательность.
3) Произведение ограниченной последовательности на бесконечно-малую равняется бесконечно-малой. последовательности.
Пусть 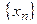 - ограниченная последовательность
- ограниченная последовательность 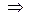
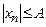
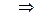
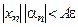
4) Произведение бесконечно-малой последовательности на бесконечно-малую равняется бесконечно-малой последовательности.
Ещё одно определение сходящейся последовательности:
Последовательность 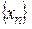 называется сходящейся, если
называется сходящейся, если 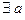 , что в
, что в 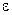 -окрестности точки
-окрестности точки 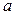 находятся все элементы этой последовательности, начиная с некоторого номера (который, конечно, зависит от
находятся все элементы этой последовательности, начиная с некоторого номера (который, конечно, зависит от 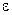 ), т.е.
), т.е.
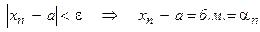
Отсюда 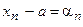 элемент бесконечно малой последовательности. Тогда любой элемент сходящейся последовательности, имеющей предел
элемент бесконечно малой последовательности. Тогда любой элемент сходящейся последовательности, имеющей предел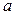 , может быть представлен в специальном виде
, может быть представлен в специальном виде 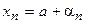
 2014-02-09
2014-02-09 504
504








