Исследование функций

01: Точка 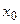– точка максимума функции 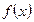, если 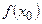наибольшее значение функции в некоторой окрестности точки 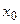, т.е. " , .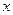

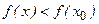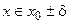02: Точка 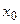– точка минимума функции 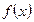, если 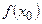наименьшее значение функции в некоторой окрестности точки 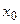, т.е. ",.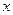

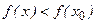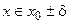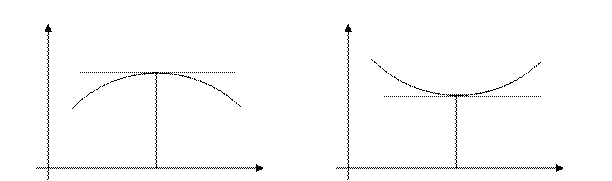
03: Точки max и min – точки экстремума.

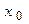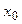max и min – это наибольшее не на отрезке, а в 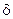-окрестности точки .

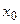Теорема 1. (Необходимое условие существования экстремума).

Если дифференцируемая функция имеет при 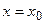max или min Þ .

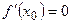Доказательство.

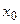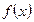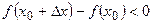Пусть для определенности в точке - max Þ 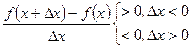Þ Þ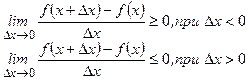

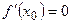
(Аналогично, если 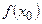- min).

На графике функции точкам экстремума соответствует вершины и впадины линии.

Касательная к графику функции в точке экстремума параллельна оси .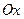

Условие не является достаточным, т.е. обратное утверждение неверно. Не при всяком значении 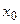, где 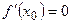обязательным будет max или min. (Пример: ).

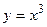В тех случаях, когда производная не существует, могут быть max и min или не то ни другое, как, например:

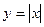
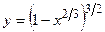
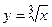
Определение. Точки, в которых производная равна 0 или не существует, называются критическими.

Теорема 2. (1-е достаточное условие существования экстремума).

Пусть функция непрерывна в некоторой окрестности точки 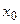и дифференцируема всюду в этой окрестности, кроме может быть самой точки .

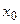· Если при переходе через эту точку слева на право производная меняет знак с <+> на <->, то при 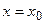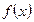- имеет max.

· Если при переходе через эту точку слева на право производная меняет знак с <-> на <+>, то при 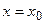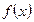- имеет min.

Доказательство.

1). Пусть 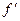меняет знак с <+> на <->, т.е. .

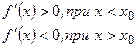По теореме Лагранжа 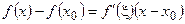, где 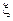- точка между 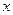и .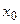

а). Если , , <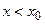

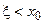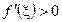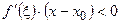
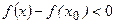
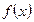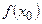
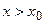
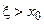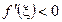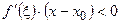
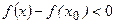
б). Если , , 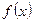<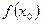. Т.е. в точке х₀ _- max.

(Для min аналогично).