Теорема 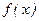Коши (об отношении приращений двух функций)

Теорема. Если и 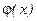непрерывны на 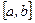и дифференцируемы во всех его внутренних точках, причем 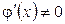(нигде), то внутри этого отрезка найдется точка 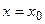, для которой:

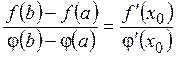, где

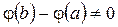, т.к. тогда по теореме Роля 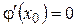, что противоречит условию теоремы.

Доказательство.

Введем вспомогательную функцию, подобную той, что в теореме Лагранжа. Обозначим .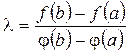

Пусть .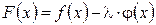

Эта функция удовлетворяет всем условиям теоремы Роля: непрерывность и дифференцируемость следует из непрерывности и дифференцируемост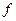и и 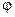. Равенство значений на концах отрезка проверяется:

,

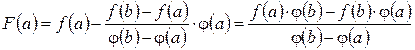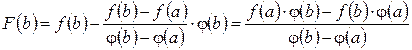
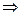
по теореме Ролля в интервале $ точка 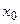, что .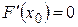

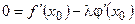
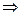
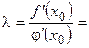
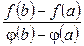
При 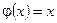теорема Коши = теореме Лагранжа.

Но теорему Коши нельзя доказать применением теоремы Лагранжа к числителю и знаменателю, т.к. промежуточная точка 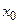в числителе и знаменателе не обязательно совпадут.