Наибольшее и наименьшее значения функции на отрезке.
Если 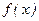 непрерывна на отрезке
непрерывна на отрезке 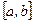 , то по свойствам непрерывности функций она достигает на этом отрезке наибольшего значения.
, то по свойствам непрерывности функций она достигает на этом отрезке наибольшего значения.
Варианты: (Если имеется конечное число критических точек).
Наибольшее значение функция достигает:
1. в одной из критических точек;
2. на концах отрезка.
То же и о наименьшем значении.
Определение. Дуга кривой называется выпуклой, если все ее точки лежат по одну сторону от касательной, проведенной в любой точке дуги.
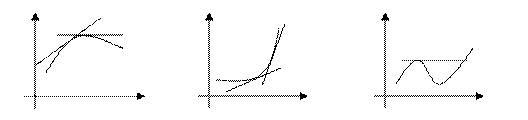
Выпуклость вверх – выпуклая, вниз – вогнутая.
В современной математике – наоборот. (Теория оптимизации).
Теорема 1. Если 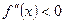 во всех точках
во всех точках 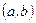 , то кривая
, то кривая 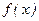 на этом интервале выпуклая.
на этом интервале выпуклая.
Доказательство.
Пусть 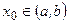 Проведем в этой точке касательную к кривой. Мы должны доказать, что все точки кривой на интервале
Проведем в этой точке касательную к кривой. Мы должны доказать, что все точки кривой на интервале 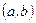 лежат ниже касательной.
лежат ниже касательной.
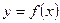 - уравнение кривой.
- уравнение кривой.
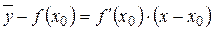 - уравнение касательной
- уравнение касательной
или 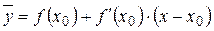 .
.
Найдем разность ординат кривой и касательной

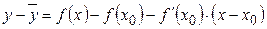 .
.
Применим теорему Лагранжа:
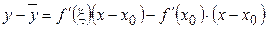 , где
, где 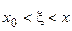

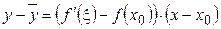 , (снова по теореме Лагранжа).
, (снова по теореме Лагранжа).
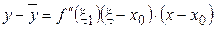 ,
, 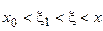 .
.
Пусть 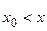 ,
, 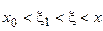

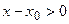 ,
, 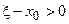 . Кроме того, по условию
. Кроме того, по условию 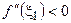

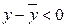 , т.е. все точки лежат ниже касательной Þ кривая выпуклая.
, т.е. все точки лежат ниже касательной Þ кривая выпуклая.
Теорема 2. Если 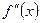 >0 во всех точках
>0 во всех точках 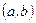 , то кривая
, то кривая 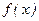 на этом интервале вогнутая.
на этом интервале вогнутая.
(Доказательство аналогично).
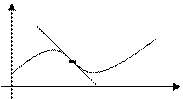
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
В точке перегиба касательная должна пересекать кривую, т.к. с одной стороны кривая лежит под касательной, с другой – над ней.
 |
Теорема 3. Если 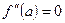 или
или 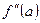 не существует и при переходе через
не существует и при переходе через 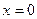
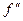 меняет знак, то
меняет знак, то 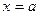 – точка перегиба.
– точка перегиба.
Доказательство.
1. Пусть 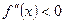 при
при 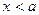 ,
, 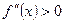 при
при 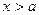 .
.  при
при 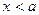 выпуклая, при
выпуклая, при 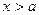 вогнутая.
вогнутая. 
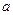 – перегиб.
– перегиб.
2. 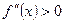 при
при 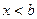 и
и 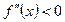 при
при 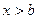
 "
" 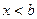
 вогнутая, при
вогнутая, при 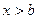 выпуклая.
выпуклая. 
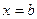 точка перегиба.
точка перегиба.
Пример. Определить точки перегиба и интервалы выпуклости.
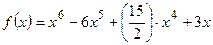
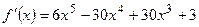
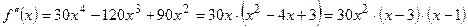
точки 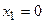
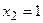
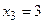 - критические точки II рода.
- критические точки II рода.
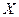
| 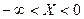
| 
| 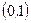
| 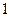
| 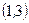
| 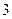
| 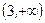
|
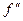
| + | + | - | + | |||
| È | не т.п. | È | т.п. | Ç | т.п. | È |
 2014-02-09
2014-02-09 574
574








