Монотонность. Условие возрастания и убывания функции

Исследование функций.

Монотонность. Условие возрастания и убывания функции. 2

Исследование функций. 2

Исследование функций с помощью 1-го достаточного признака экстремума. 5

Наибольшее и наименьшее значения функции на отрезке. 7

Выпуклость и вогнутость. Точки перегиба. 7

Исследование функций.

Теорема. (Необходимый и достаточный признаки монотонности функции).

Необходимость. Если 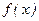, имеющая производную на отрезке 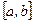, возрастает на этом отрезке (убывает), то ее производная на этом отрезке не отрицательна, т.е. 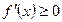(не положительна, ).

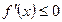Доказательство.

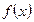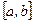
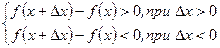
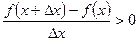
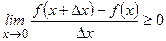Если возрастает на отрезке в обоих случаях (по теореме о пределах – сохранение знака), т.е. .

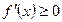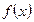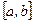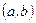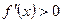
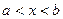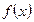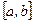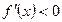
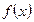Достаточность. Если непрерывна на отрезке и дифференцируема на интервале , причем , то ­ на (¯ на ).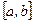

Доказательство.

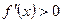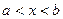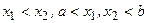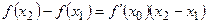
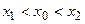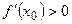
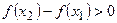
Пусть при . Если , то из теоремы Лагранжа о конечных приращениях следует, что . Т.к. ­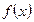. (Аналогично для убывания).