Определение. Прямая А называется асимптотой кривой, если расстояние d от некоторой точки М Î кривой до этой прямой стремится к нулю при стремлении точки М к ¥.
Рассмотрим случаи вертикальной и наклонной асимптот.
1. Вертикальная асимптота: уравнение 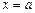
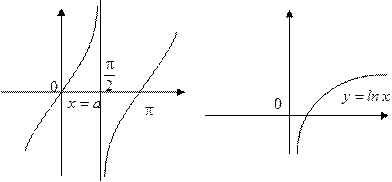 |
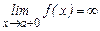 или
или 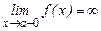 или
или 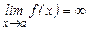 Þ
Þ 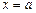 – асимптота.
– асимптота.
Т. е. для отыскания вертикальных асимптот нужно найти такие 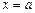 , при которых
, при которых 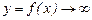 .
.
2. Наклонные асимптоты: уравнение 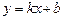
Для того, чтобы найти уравнение наклонной асимптоты нужно найти числа 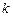 и
и 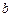 .
.
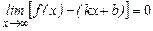 (*),
(*),
т.е. 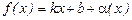 | делим на
| делим на 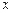 и переходим к
и переходим к 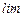
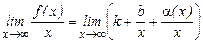
при 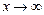 ,
, 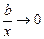 ,
, 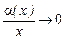 Þ
Þ 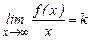 (**)
(**)
из (*) Þ 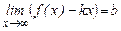 (***)
(***)
То есть, если 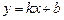 , то
, то 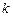 и
и 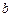 находятся по формулам (**) и (***). Если хотя бы один из пределов не существует, то кривая асимптоты не имеет.
находятся по формулам (**) и (***). Если хотя бы один из пределов не существует, то кривая асимптоты не имеет.
Пример 1. 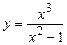
1). Вертикальные асимптоты 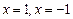
2). Наклонные асимптоты
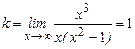
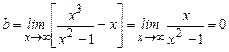
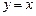 - наклонная асимптота.
- наклонная асимптота.
Пример 2. 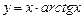
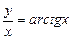 , при
, при 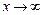 ,
, 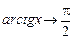
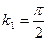
при 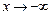 ,
, 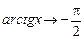
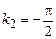
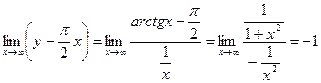
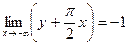
Первая асимптота: 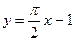 .
.
Вторая асимптота: 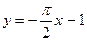 .
.
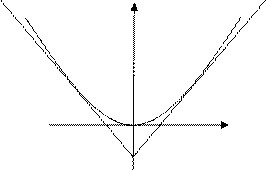
Чтобы построить:
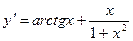 ,
, 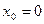 ,
, 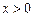 ,
, 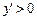 Þ
Þ 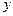 h
h
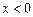 ,
, 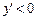 Þ
Þ 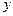
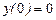
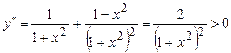 Þ È.
Þ È.
Обратно: если существуют пределы (**) и (***) Þ выполняется равенство (*) Þ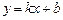 – асимптота.
– асимптота.
Асимптотическое изменение функций может быть различным при 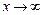 и
и 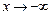 Þ рассматривать оба случая отдельно.
Þ рассматривать оба случая отдельно.
После того как найдена асимптота, исследованием знака выражения 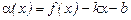 для больших значений
для больших значений 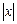 устанавливается взаимное расположение функций и асимптоты:
устанавливается взаимное расположение функций и асимптоты:
- функция над асимптотой 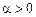 ,
,
- функция под асимптотой 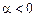 ,
,
- функция не ограниченное число раз пересекает асимптоту (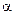 - меняет знак бесконечное число раз).
- меняет знак бесконечное число раз).
Общая схема исследования функций.
I. 1). Область определения;
2). Точки разрыва и интервал непрерывности;
3). Поведение функций в окрестностях точек разрыва, вертикальные асимптоты;
4). Точки пересечения графика с осями координат;
5). Симметрия графика (четность или нечетность функций);
6). Периодичность функции.
II. 1). Точки экстремума;
2). Интервалы монотонности;
3). Экстремальные значения функции.
III. Интервалы выпуклости и вогнутости. Точки перегиба.
IV. Поведение функции на бесконечности. Наклонные (в частности, горизонтальные) асимптоты.
 2014-02-09
2014-02-09 641
641








