Простейшим итерационным методом для решения СЛАУ является метод простой итерации (МПИ), основным недостатком которого является его низкя скорость сходимости. Здесь исходная СЛАУ (1) преобразуется к виду
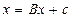 (2)
(2)
где 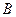 -
- 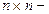 матрица,
матрица, 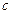 - вектор длины
- вектор длины 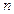 , а решение СЛАУ (2) находится как предел последовательности
, а решение СЛАУ (2) находится как предел последовательности
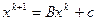 (3)
(3)
Ключевым вопросом при изучени итерационных методов является вопрос их сходимости (к точному решению СЛАУ). Надо выяснить, каким условиям должна удовлетворять матрица 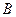 в (2) и (3), чтобы итерационный процесс (3) сходился.
в (2) и (3), чтобы итерационный процесс (3) сходился.
Лемма 1. Для того, чтобы матричный ряд
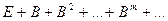
где 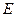 - единичная
- единичная 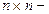 матрица, сходился, необходимо и достаточно, чтобы все собственные значения (СЗ)
матрица, сходился, необходимо и достаточно, чтобы все собственные значения (СЗ) 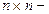 матрицы
матрицы 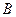 по модулю были меньше 1:
по модулю были меньше 1:
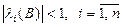 .
.
При выполнении этого условия матрица 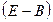 имеет обратную, и справедливо равенство:
имеет обратную, и справедливо равенство:
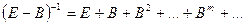
Лемма 2. Для того, чтобы 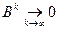 необходимо и достаточно, чтобы чтобы все СЗ матрицы
необходимо и достаточно, чтобы чтобы все СЗ матрицы 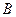 по модулю были меньше 1.
по модулю были меньше 1.
Лемма 3. Модули собственных значений матрицы не превосходят любую из ее норм.
Теорема 1 (критерий сходимости МПИ). Для того, чтобы векторная последовательность 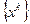 , построенная по формуле (3), сходилась при любом начальном приближении
, построенная по формуле (3), сходилась при любом начальном приближении 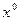 к решению СЛАУ (1) (и (2)), необходимо и достаточно, чтобы все СЗ матрицы
к решению СЛАУ (1) (и (2)), необходимо и достаточно, чтобы все СЗ матрицы 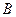 по модулю были меньше 1.
по модулю были меньше 1.
Доказательство. Достаточность. Найдем точное решение 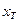 СЛАУ (2):
СЛАУ (2):
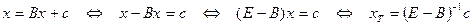 .
.
Найдем выражение для 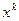 в формуле (3) через
в формуле (3) через 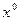 :
:
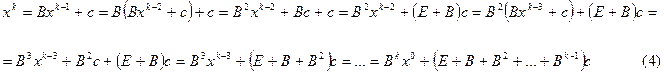
По лемме 1 матричный ряд 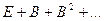 в правой части (4) сходится к матрице
в правой части (4) сходится к матрице 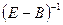 , кроме того в силу необходимого условия сходимости ряда его k -ый член стремится к нулю, т.е.
, кроме того в силу необходимого условия сходимости ряда его k -ый член стремится к нулю, т.е.
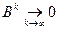 .
.
Тогда переходя к пределу при 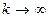 в формуле (4), получим:
в формуле (4), получим:
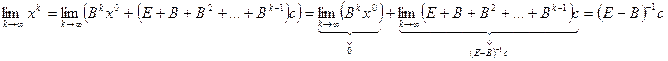
Таким образом,
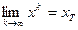 ,
,
что и требовалось доказать.
Необходимость. Пусть для любого начального приближения 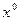 векторная последовательность
векторная последовательность 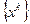 , построенная по формуле (3), сходится к
, построенная по формуле (3), сходится к 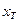 :
: 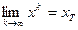 . Рассмотрим
. Рассмотрим
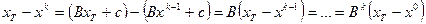 . (5)
. (5)
Поскольку 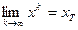 , то
, то 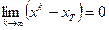 . Поэтому, если в (5) перейти к пределу, получим:
. Поэтому, если в (5) перейти к пределу, получим:
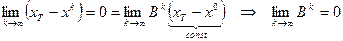 .
.
Тогда в соответствии с леммой 2 из последнего равенства следует, что все СЗ матрицы 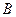 по модулю были меньше 1, что и требовалось показать.
по модулю были меньше 1, что и требовалось показать.
Применение доказанной теоремы требует знание границ спектра (спектр – множество собственных значений) матрицы 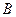 . На практике эти границы не всегда можно легко определить, поэтому сформулируем еще некоторые достаточные условия сходимости МПИ.
. На практике эти границы не всегда можно легко определить, поэтому сформулируем еще некоторые достаточные условия сходимости МПИ.
Теорема 2. Для того, чтобы векторная последовательность 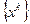 , построенная по формуле (3), сходилась к решению СЛАУ (1) (и (2))
, построенная по формуле (3), сходилась к решению СЛАУ (1) (и (2)) 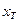 , достаточно, чтобы какая-либо норма матрицы
, достаточно, чтобы какая-либо норма матрицы 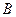 была меньше 1:
была меньше 1:
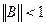 .
.
Доказательство очевидно вытекает из предыдущей теоремы и леммы 3.
Следствие. Если для матрицы 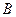 выполняется
выполняется
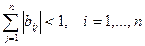 ,
,
или
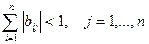 ,
,
то
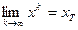 .
.
Предположим, что МПИ, построенный по формуле (3) для решения СЛАУ (1) (и (2)) сходится. В общем случае итерационный процесс (3) даст точное решение 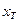 за бесконечное число итераций. В силу этого при решении СЛАУ итерационным методом с самого начала задается абсолютная погрешность
за бесконечное число итераций. В силу этого при решении СЛАУ итерационным методом с самого начала задается абсолютная погрешность 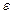 , приемлемая для получаемого приближенного решения. На каждом итерационном шаге происходит проверка достижения заданной точности. Эта проверка может происходить следующим образом: если
, приемлемая для получаемого приближенного решения. На каждом итерационном шаге происходит проверка достижения заданной точности. Эта проверка может происходить следующим образом: если 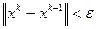 , то итерационный процесс завершается, и
, то итерационный процесс завершается, и 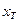 полагается равным
полагается равным 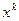 , иначе переход на очередной итерационный шаг.
, иначе переход на очередной итерационный шаг.
Пусть матрица 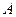 СЛАУ (1) имеет диагональное преобладание по строкам, т.е. для ее элементов выполняются соотношения:
СЛАУ (1) имеет диагональное преобладание по строкам, т.е. для ее элементов выполняются соотношения:
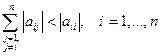 .
.
Тогда переход от вида (1) к виду (2) СЛАУ, определяющему сходящийся МПИ, можно провести следующим образом:
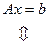
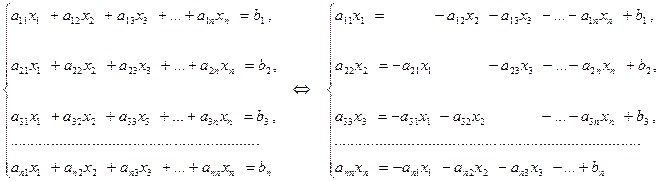
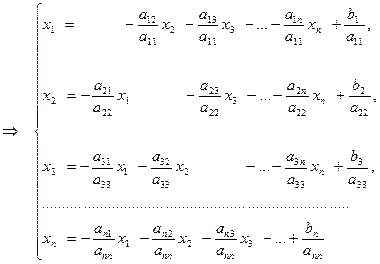
Последняя система имеет уже вид (2), для которого
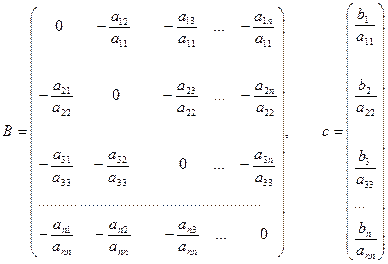 .
.
Поскольку для исходной матрицы 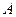 в силу ее диагонального преобладания выполнялись соотношения
в силу ее диагонального преобладания выполнялись соотношения 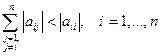 , то при делении каждого i -го соотношения на
, то при делении каждого i -го соотношения на 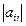 получим:
получим:
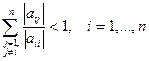 .
.
А значения 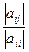 - это значения модулей внедиагональных элементов полученной выше матрицы
- это значения модулей внедиагональных элементов полученной выше матрицы 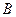 :
:
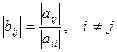 .
.
Тогда для полученной матрицы 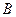 выполняются соотношения:
выполняются соотношения:
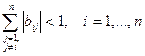 ,
,
Но учитывая, что 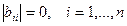 , последние неравенства можно переписать в виде:
, последние неравенства можно переписать в виде:
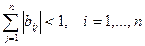 ,
,
а это означает (по следствию из теоремы 2), что МПИ сходится к точному решению СЛАУ (1):
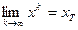 .
.
Замечание 1. МПИ является одним из самых медленных итерационных методов решения СЛАУ.
Замечание 2 (вычислительная сложность МПИ). Основная расчетная формула МПИ – это формула (3): 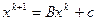 , которая определяет действия данного алгоритма на каждой итерации. Очевидно, что эти действия сводятся к умножению
, которая определяет действия данного алгоритма на каждой итерации. Очевидно, что эти действия сводятся к умножению 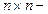 матрицы на вектор длины
матрицы на вектор длины 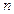 (
(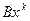 ), что потребует
), что потребует 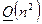 операций, и к последующему сложению двух векторов длины
операций, и к последующему сложению двух векторов длины 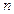 (
(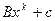 ), что потребунт еще
), что потребунт еще 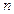 операций. В итоге, каждая итерация МПИ требует
операций. В итоге, каждая итерация МПИ требует 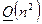 операций, тогда в целом количество арифметических операций, необходимых для решения СЛАУ МПИ, определиться как
операций, тогда в целом количество арифметических операций, необходимых для решения СЛАУ МПИ, определиться как
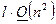 ,
,
где 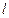 - это количество итераций, затраченных в МПИ для достижения заданной точности решения
- это количество итераций, затраченных в МПИ для достижения заданной точности решения 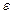 . Очевидно, что в итоге вычислительная сложность МПИ (как и любого другого итерационного метода) определяетсяколичеством итераций
. Очевидно, что в итоге вычислительная сложность МПИ (как и любого другого итерационного метода) определяетсяколичеством итераций 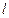 .
.
 2014-02-09
2014-02-09 7311
7311
