Итерационные методы (метод Якоби, метод Зейделя, метод релаксации)

Итерационные методы решения СЛАУ позволяют найти решение лишь с заданной точностью. Пусть требуется решить систему Ax=f. Представим матрицу A в виде A=L+D+U, где L - нижнетреугольная матрица, D - диагональная матрица, U - верхнетреугольная матрица.

Запишем систему (6.1) в развернутом виде:

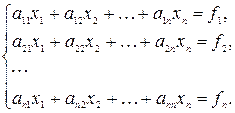
где 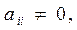(i=1,2,…,n), и приведем к виду

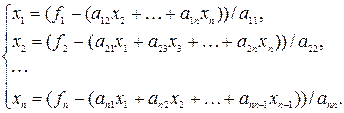
Обозначим

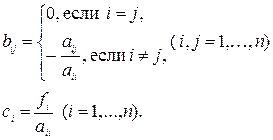
В векторно-матричном виде система запишется в виде:

x=B x+C,

где B= { b_ij } _i,j=1,…,n, C= { c_i } _i=1,…,n, x=(x₁,x₂,…,x_n)^Т.

Построим итерационный процесс по формуле

x^(k+1)=B x^(k)+C,

где x⁰ - задано, k - номер итерации, x^(k)=(x₁^k,x₂^k,…,x_n^k)^Т.

В качестве условия остановки итерационного процесса, можно использовать условие

,

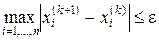где e - заданная точность вычисления.

Достаточным условием сходимости метода простой итерации является:

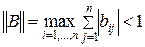
или условие диагонального преобладания матрицы A, т. е.

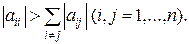
Необходимым и достаточным условием сходимости итерационных методов является условие max | li (B)| < 1. Оценка погрешности итерационного процесса запишется в виде:

,

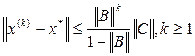где x^*- точное решение. Определяя необходимое число итераций для достижений заданной точности из формулы, получим

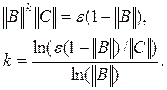
Итерационная формула метода Якоби имеет вид:

,

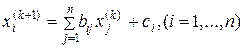где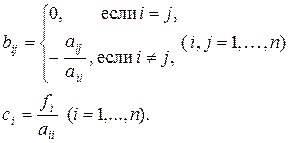

Для метода Зейделя каждый вычисленный элемент вектора x на (k+1) -й итерации используется при вычислении следующего элемента:

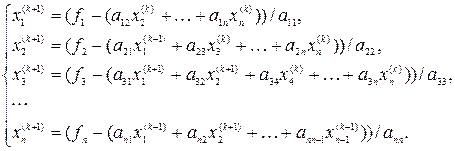
В общем виде получим:

.

Для метода релаксации введем числовой параметр w так, что

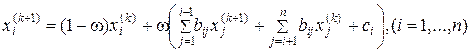
при w > 1 будет метод верхней релаксации,

при w = 1 - метод полной релаксации (метод Зейделя),

при w < 1 - метод нижней релаксации.

Если A=A^* > 0, a w такое, что 0< w <2, то метод релаксации сходится. Параметр w выбирается из условия минимума спектрального радиуса оператора перехода от итерации к итерации.