Пусть в плоскости Oxy имеется круг радиуса R с центром в начале координат и на его окружности задана некоторая функция 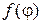 , где j - полярный угол. Требуется найти функцию u (r, j), непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа
, где j - полярный угол. Требуется найти функцию u (r, j), непрерывную в круге, включая границу, удовлетворяющую внутри круга уравнению Лапласа
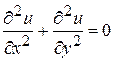 (1)
(1)
и на окружности круга принимающую заданные значения
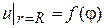 .
.
Задача (1) очень важна в физических приложениях. Ее можно интерпретировать как задачу нахождения электростатического потенциала внутри круга по известному распределению потенциала на границе. Другая интерпретация – модель мыльной пленки. Если сделать из проволоки кольцо и изогнуть его так, чтобы изгиб задавался функцией 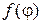 , а затем погрузить в мыльный раствор, то мыльная пленка натянется в соответствии с формой проволоки. Возвышения точек пленки описываются решением задачи (1), если смещения малы. Будем решать задачу в полярных координатах. Перепишем уравнение (1) в этих координатах:
, а затем погрузить в мыльный раствор, то мыльная пленка натянется в соответствии с формой проволоки. Возвышения точек пленки описываются решением задачи (1), если смещения малы. Будем решать задачу в полярных координатах. Перепишем уравнение (1) в этих координатах:

или
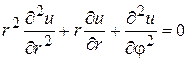 . (2)
. (2)
Будем искать решение методом разделения переменных, полагая
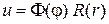 . (3)
. (3)
Подставляя в уравнение (2), получим:

или
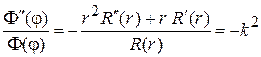 . (4)
. (4)
Так как левая часть этого равенства не зависит от r, а правая от j, следовательно, они равны постоянному числу, которое мы обозначаем через 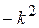 . Таким образом, равенство (4) дает два уравнения:
. Таким образом, равенство (4) дает два уравнения:
 , (5)
, (5)
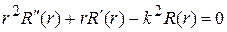 . (6)
. (6)
Общее решение уравнения (5) будет
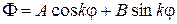 . (7)
. (7)
Уравнение (6) – есть уравнение Эйлера. Ищем его решение в виде  . Подставляя
. Подставляя  в (6), получим:
в (6), получим:
 .
.
Сокращая это уравнение на 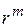 , получаем
, получаем 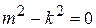 , то есть,
, то есть,  .
.
Итак, имеются два частных линейно независимых решения 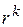 и
и  . Общее решение уравнения (6) будет
. Общее решение уравнения (6) будет
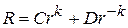 . (8)
. (8)
Выражения (7) и (8) подставляем в (3):
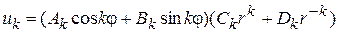 . (9)
. (9)
Функция (9) будет решением уравнения (2) при любом значении k, отличном от нуля. Если k = 0, то уравнения (5) и (6) принимают вид:
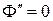 ,
, 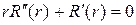 ,
,
и, следовательно,
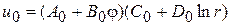 . (10)
. (10)
Решение должно быть периодической функцией от j, так как при одном и том же значении r при j и j + 2p мы должны иметь одно и то же значение решения, потому что рассматривается одна и та же точка круга. Поэтому очевидно, что в формуле (10) должно быть  . Далее, мы ищем решение, непрерывное и конечное в круге. Следовательно, в центре круга при r = 0 решение должно быть конечным, и потому в формуле (10) должно быть
. Далее, мы ищем решение, непрерывное и конечное в круге. Следовательно, в центре круга при r = 0 решение должно быть конечным, и потому в формуле (10) должно быть  , а в формуле (9)
, а в формуле (9)  .
.
Таким образом, правая часть (10) обращается в произведение 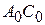 , которое мы обозначим через
, которое мы обозначим через 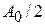 . Итак,
. Итак,
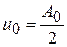 .
.
Мы будем составлять решение нашей задачи в виде суммы решений вида (9), так как в силу линейности и однородности уравнения Лапласа сумма решений есть также решение. Сумма должна быть периодической функцией от j. Это будет так, если каждое слагаемое будет периодической функцией от j. Для этого k должно принимать целые значения. Мы можем ограничиться только положительными значениями  так как в силу произвольности постоянных A, B, C, D отрицательные значения k новых частных решений не дают. Итак,
так как в силу произвольности постоянных A, B, C, D отрицательные значения k новых частных решений не дают. Итак,
 (11)
(11)
(постоянная  включена в
включена в  и
и  ). Подберем теперь произвольные постоянные
). Подберем теперь произвольные постоянные  и
и  так, чтобы удовлетворялось краевое условие
так, чтобы удовлетворялось краевое условие 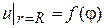 . Подставляя в равенство (11)
. Подставляя в равенство (11) 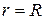 , получаем:
, получаем:
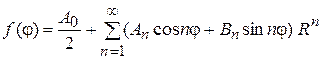 . (12)
. (12)
Чтобы имело место равенство (12) нужно, чтобы функция 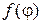 разлагалась в ряд Фурье в интервале (-p, p) и чтобы
разлагалась в ряд Фурье в интервале (-p, p) и чтобы 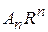 и
и 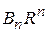 были ее коэффициентами Фурье. Следовательно,
были ее коэффициентами Фурье. Следовательно,  и
и  должны определяться по формулам:
должны определяться по формулам:
 ,
, 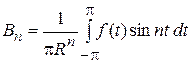 . (13)
. (13)
Итак, ряд (11) с коэффициентами, определенными по формулам (13), будет решением нашей задачи, если он допускает двукратное дифференцирование по r и j.
Интегральная формула Пуассона. Преобразуем формулу (11). Подставляя вместо  и
и  их выражения (13) и произведя тригонометрические преобразования, получим:
их выражения (13) и произведя тригонометрические преобразования, получим:

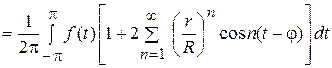 . (14)
. (14)
Преобразуем выражение, стоящее в квадратных скобках:

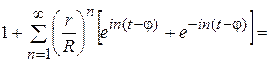
=
=
=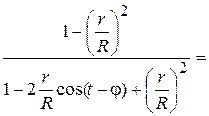
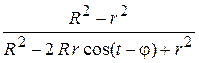 . (15)
. (15)
Заменяя выражение, стоящее в квадратных скобках в формуле (14), выражением (15), получим:
 . (16)
. (16)
Формула (16) называется интегралом Пуассона.
 2014-02-10
2014-02-10 1329
1329







