Фундаментальные решения уравнения Лапласа
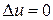 ,
,
где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно
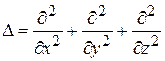 ; (1)
; (1)
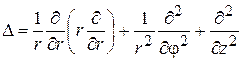 ; (2)
; (2)
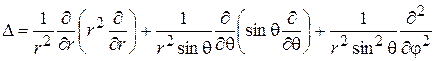 . (3)
. (3)
Важную роль при решении задач для уравнений Лапласа и Пуассона представляет решение уравнения Лапласа, обладающие сферической или цилиндрической симметрией.
Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 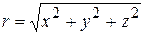 точки
точки 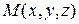 до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид
до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид
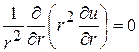 . (4)
. (4)
Интегрируя уравнение (13), получим
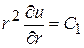 ,
, 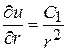 ,
, 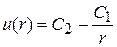 .
.
При 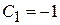 и
и 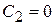 получаем функцию
получаем функцию
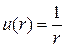 , (5)
, (5)
которая удовлетворяет уравнению Лапласа всюду, кроме точки 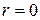 , где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве. С точностью до множителя пропорциональности она совпадает с полем точечного заряда e, помещенного в начале координат, потенциал этого поля равен
, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве. С точностью до множителя пропорциональности она совпадает с полем точечного заряда e, помещенного в начале координат, потенциал этого поля равен
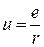 .
.
В задаче с осевой симметрией, когда функция u в цилиндрической системе координат не зависит от j и z, уравнение Лапласа имеет вид
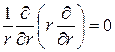 . (6)
. (6)
Интегрируя уравнение (6), находим
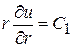 ,
, 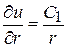 ,
, 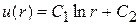 .
.
Полагая 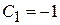 и
и 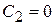 , будем иметь
, будем иметь
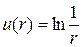 ,
, 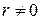 .
.
Эту функцию называют фундаментальным решением уравнения Лапласа на плоскости. Аналогично, функция 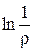 удовлетворяет уравнению Лапласа всюду, кроме точки
удовлетворяет уравнению Лапласа всюду, кроме точки 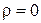 , где она обращается в бесконечность, и с точностью до множителя совпадает с полем заряженной линии, потенциал которого равен
, где она обращается в бесконечность, и с точностью до множителя совпадает с полем заряженной линии, потенциал которого равен
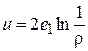 ,
,
где 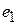 - плотность заряда, рассчитанная на единицу длины.
- плотность заряда, рассчитанная на единицу длины.
 2014-02-10
2014-02-10 2226
2226
