2014-02-02
4759
Определение 5.2. Пусть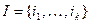 
и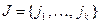 
множества номеров строк и столбцов матрицы A, соответственно. Подматрицу матрицы A, расположенную на пересечении строк с номерами из I и столбцов с номерами из J, обозначим как 
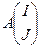, а подматрицу, получаемую из A, вычеркиванием строк с номерами из I и столбцов с номерами из J обозначим через 
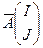. Определитель 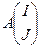называется минором, а определитель 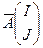- дополнительным минором.
Лемма 5.1 Справедливо равенство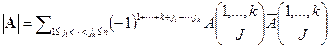 
.
Доказательство. Выразим правую часть равенства через элементы исходной матрицы. Для этого заметим, что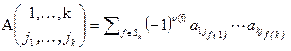 
и 
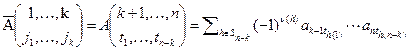, где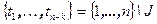 
(номера 
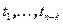упорядочены в порядке возрастания). Подставим данные выражения в правую часть и перемножим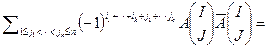 
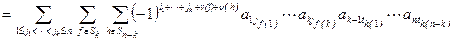
Первая сумма состоит из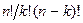 
слагаемых, вторая сумма – из k! слагаемых и третья сумма – (n-k)! слагаемых. Следовательно, общее количество слагаемых равно n!. Покажем, что каждое из этих слагаемых входит в определитель с тем же самым знаком. Слагаемое имеет вид 
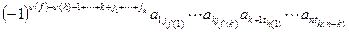, где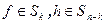 
. В определителе оно соответствует подстановке 
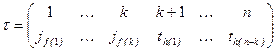. Представим подстановку 
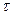в виде произведения трёх подстановок 
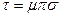, где 
, 
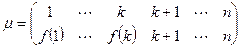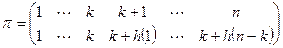и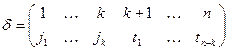 
. Легко убедиться в справедливости равенств 
, 
, 
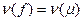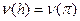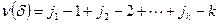. Следовательно, 
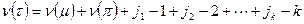, и таким образом, совпадение знаков показано, что завершает доказательство леммы.
Теорема 5.1 (Лапласа). Пусть 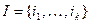множество номеров строк. Справедливо равенство 
.
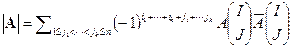Доказательство. Обозначим через B матрицу, получающуюся из матрицы A последовательной подстановкой строк с номерами из I на место первых k строк (при этом порядок остальных строк не нарушается). Для этого потребуется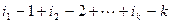 
подстановок строк, и значит, 
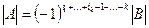. Разложив определитель матрицы B (Лемма 5.1), и заметив, что 
, 
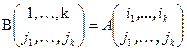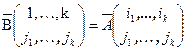выводим .
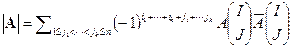Следствие 5.1. Пусть 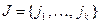множество номеров столбцов. Справедливо равенство 
.
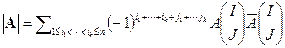Вытекает из теоремы Лапласа и равенства определителей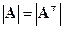 
.
Следствие 5.2. (разложение по столбцу). Пусть j – номер столбца. Справедливо равенство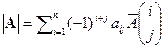 
.
Следствие 5.3 (разложение по строке) Пусть i – номер строки. Справедливо равенство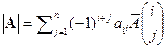 
.
Примеры использования теоремы Лапласа.
