Понятие о линейной независимости функций

Определение. Функции y₁, y₂,…, y_n называются линейно независимыми в интервале (a,b), если между ними не существует соотношения вида: 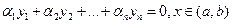(1), где 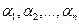- постоянные числа, не равные нулю одновременно. В противном случае функции 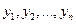называются линейно зависимыми.

Очевидно, что если одна из функций 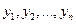тождественно равна нулю в интервале (a,b), то эти функции линейно зависимы в (a,b).

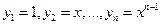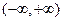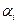Пример 1. Функции (2) линейно независимы в интервале . Соотношение в котором не все равны нулю, не может выполняться тождественно, так как уравнение n-1 степени не может иметь более чем n-1 корней.

Пример 2. Пусть 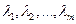- различные числа. Тогда функции

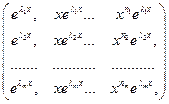(3), где n₁, n₂,…, n_m – целые неотрицательные числа, линейно независимы в интервале .

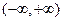Пример 3. Пусть 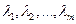- различные числа. Тогда функции

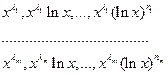(4), где n₁, n₂,…, n_m – целые неотрицательные числа, линейно

независимы в интервале .

Пример 4. Функции 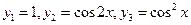линейно зависимы в интервале 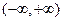, так как при всех х справедливо соотношение .

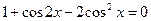Пример 5. Функции 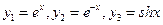линейно зависимы в интервале 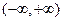, так как 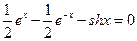справедливо при всех х.