Необходимое условие линейной зависимости n функций

Пусть функции 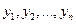, 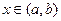имеют производные предела (n-1).

Рассмотрим определитель: 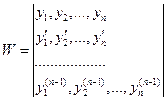(1)

W(x) называется определителем Вронского для функций .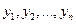

Теорема 1. Если функции 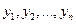линейно зависимы в интервале (a,b), то их вронскиан W(x) тождественно равен нулю в этом интервале.

Доказательство. По условию теоремы выполняется соотношение

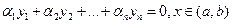, (2) где не все 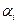равны нулю. Пусть 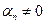. Тогда

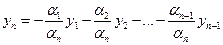(3). Дифференцируем это тождество n-1 раз и,

подставляя вместо 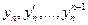их полученные значения в определитель Вронского,

получаем:

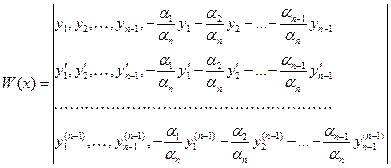(4).

В определителе Вронского последний столбец является линейной комбинацией предыдущих n-1 столбцов и поэтому равен нулю во всех точках интервала (a,b).

Теорема 2. Если функции y₁,..., y_n являются линейно независимыми решениями уравнения L[y] = 0, все коэффициенты которого непрерывны в интервале (a,b), то вронскиан этих решений отличен от нуля в каждой точке интервала (a,b).

Доказательство. Допустим противное. Существует Х₀, где W(Х₀)=0. Составим систему n уравнений

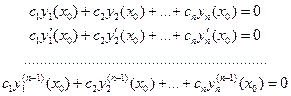(5).

Очевидно, что система (5) имеет ненулевое решение. Пусть 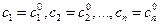(6).

Составим линейную комбинацию решений y₁,..., y_n.

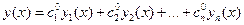(7).

У(х) является решением уравнения L[y] = 0. Кроме этого 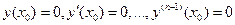. В силу теоремы единственности решения уравнения L[y] = 0 с нулевыми начальными условиями может быть только нулевым, т.е. .

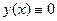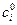Мы получаем тождество , где не все равны нулю, а это означает, что y₁,..., y_n линейно зависимы, что противоречит условию теоремы. Следовательно, нет такой точки 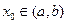где W(Х₀)=0.

На основе теоремы 1 и теоремы 2 можно сформулировать следующее утверждение. Для того, чтобы n решений уравнения L[y] = 0 были линейно независимы в интервале (a,b), необходимо и достаточно, чтобы их вронскиан не обращался в нуль ни в одной точке этого интервала.

Из доказанных теорем также следуют такие очевидные свойства вронскиана.

1. Если вронскиан n решений уравнения L[y] = 0 равен нулю в одной точке х = х₀ из интервала (a,b), в котором все коэффициенты р_i(x) непрерывны, то он равен нулю во всех точках этого интервала.
2. Если вронскиан n решений уравнения L[y] = 0 отличен от нуля в одной точке х = х₀ из интервала (a,b), то он отличен от нуля во всех точках этого интервала.

Таким образом, для линейности n независимых решений уравнения L[y] = 0 в интервале (a,b), в котором коэффициенты уравнения р_i(x) непрерывны, необходимо и достаточно, чтобы их вронскиан был отличен от нуля хоть в одной точке этого интервала.