Построение однородного линейного уравнения, имеющего заданную ФСР

Покажем, что всякой системе n непрерывно дифференцируемых и линейно независимых в интервале (a,b) функций y₁,..., y_n, вронскиан которых отличен от нуля в интервале (a,b), соответствует лишь одно уравнение L[y] = 0, для которого эта система функций будет фундаментальной.

Итак, даны y₁,..., y_n. Найти .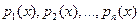

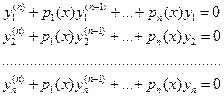(1)

Система (1) решается единственным образом, так как является линейной, неоднородной относительно неизвестных 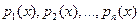, определитель которой W(x)≠0 в интервале (a,b).

Можно добавить к системе (1) ещё одно уравнение, а именно 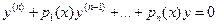(2).

Потребуем, чтобы новая система была совместна:

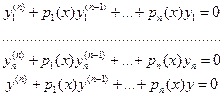(3).

Тогда 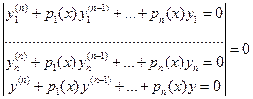(4), или 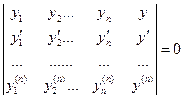(5).

Разлагая определитель (5) по элементам последнего столбца и деля все члены на W(x), мы получим искомое уравнение.

Пример.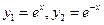

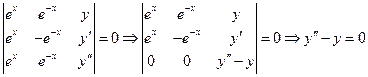
ЛЕКЦИЯ 3: