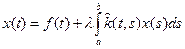Интегральное уравнение Фредгольма 2-го рода с вырожденным ядром

(1), где 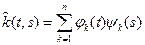(2).

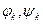- линейно независимы попарно между собой.

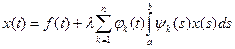(3).

Обозначим 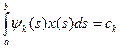(4), тогда: 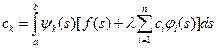(5). Здесь (k= = 1,2,...,n).

Пусть 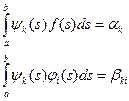(6), 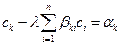, (k = 1,2,...,n) (7).

Определитель системы (7) имеет вид:

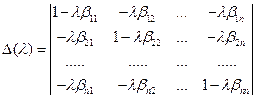(8).

Отметим, что .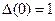

Следовательно, для достаточно малых значений 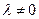существует единственное решение.

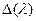- многочлен от λ степени n, имеет не более n различных корней.

Корни уравнения 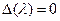называются характеристическими числами ядра k(t,s).

Если уравнение однородное, т.е. f(t)=0, или 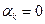, то 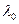корень 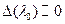является собственным значением однородного уравнения.

Для неоднородного уравнения при 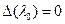возможны два случая: существует либо бесконечное множество решений, либо ни одного.