Свойства условных математических ожиданий.
1) 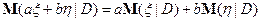
2) 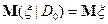 при
при 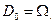
3) 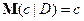
4) 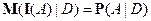
5) 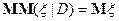 – формула полной вероятности
– формула полной вероятности
6) если 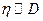 , то
, то 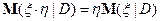 ;
; 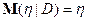 в том числе
в том числе 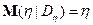
7) если 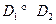 , то
, то 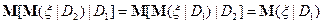
8) если  и
и 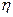 независимы, то
независимы, то 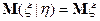
9) 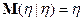
10) 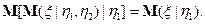
Доказательства свойств 1), 2), 3), 4), 8), 9) очевидны.
Доказательство свойства 5).
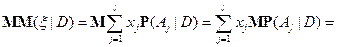
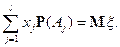
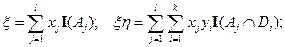
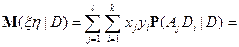
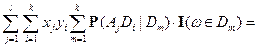
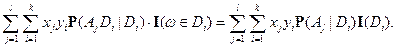
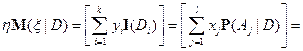
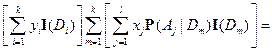
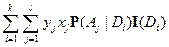
Так как 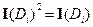 ;
; 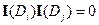 при
при 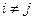 , то свойство доказано.
, то свойство доказано.
Доказательство свойства 7).
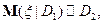
следовательно,
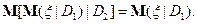
Пусть 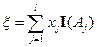 ;
; 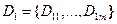 ;
; 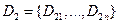 .
.
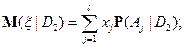
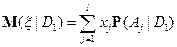 .
.
Т.е. для доказательства свойства достаточно показать, что справедлива
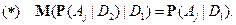
Так как
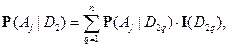
то
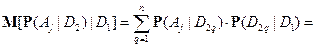
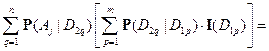
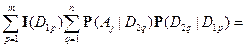
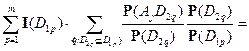
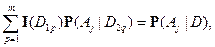
что и доказывает (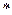 ).
).
Доказательство свойства 10) следует из 7).
Пусть 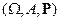 – конечное вероятностное пространство.
– конечное вероятностное пространство.
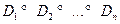 ,
, 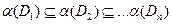 .
.
Определение. Последовательность случайных величин 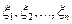 называется мартингалом относительно потока
называется мартингалом относительно потока 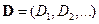 , если
, если
1) 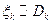
2) 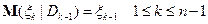 .
.
Можно считать, что 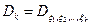 .
.
Следовательно 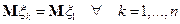 .
.
Пусть 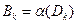 .
.
Определение. Случайная величина 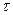 со значениями
со значениями 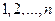 называется моментом остановки относительно потока
называется моментом остановки относительно потока 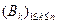
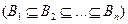 , если для любого
, если для любого 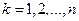 случайная величина
случайная величина 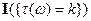
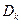 - измерима, т.е.
- измерима, т.е. 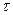 -
- 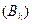 - момент остановки.
- момент остановки.
Пример.
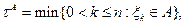
так как 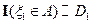 ;
; 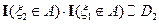 ;
; 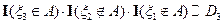 и т.д.
и т.д.
Теорема. Пусть 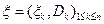 – мартингал и
– мартингал и 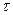 – некоторый момент остановки относительно разбиения
– некоторый момент остановки относительно разбиения 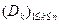 . Тогда
. Тогда
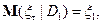
где
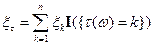
и, следовательно, 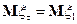 .
.
 2014-02-12
2014-02-12 358
358








