| Распределение | Плотность | Параметры |
| 1) Равномерное на [a,b] | 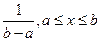 | 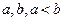 |
| 2) Нормальное гауссовское | 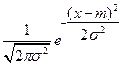 | 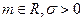 |
| 3) Экспоненциальное | 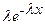 | 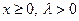 |
| 4) Двустороннее экспоненциальное | 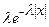 | 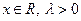 |
5) Хи-квадрат 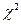 | 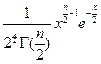 | 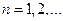 |
| 6) Стьюдента, t | 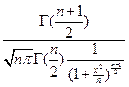 | 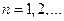 |
| 7) Коши | 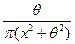 | 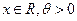 |
Обобщения для векторной случайной величины со значениями в 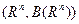
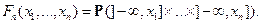
Определим разностный оператор 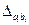 при
при 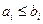
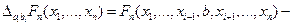
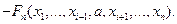
Тогда любая функция, удовлетворяющая свойствам 1) - 4) может служить функцией распределения:
1) 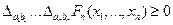
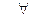
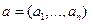 ,
, 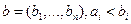
2) если 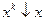 при
при 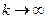 , то
, то 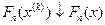 при
при 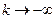
3) 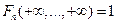
4) 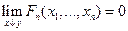 , если хотя бы одна из координат
, если хотя бы одна из координат 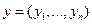 равна
равна 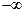 .
.
В частном абсолютно-непрерывном случае
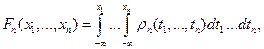
где 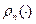 – плотность, т.е.
– плотность, т.е.
1) 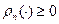 ,
,
2) 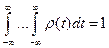 .
.
Пример. Так в случае 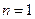
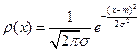
с 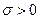 – нормальное (гауссовское) распределение и плотность
– нормальное (гауссовское) распределение и плотность 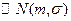 . Если
. Если 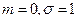 ,
, 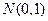 – стандартное распределение.
– стандартное распределение.
При 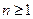
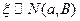 (положительно определенная матрица
(положительно определенная матрица 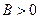 )
)
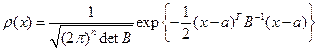
(забегая вперед заметим, что 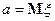 ,
, 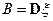 ).
).
Пусть на 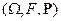 заданы
заданы 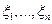 – случайные величины со значениями в
– случайные величины со значениями в 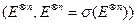 , т.е.
, т.е. 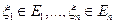 ;
;
Определение. Случайные величины 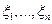 независимы, если для любых
независимы, если для любых 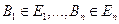
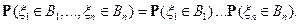
Предложение. 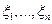 независимы тогда и только тогда, когда для любого
независимы тогда и только тогда, когда для любого 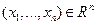
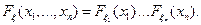
Пример.
1) Пусть 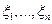 – независимые нормально распределенные случайные величины. Распределение
– независимые нормально распределенные случайные величины. Распределение 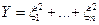 называется
называется 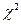 - распределением с
- распределением с 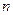 степенями свободы.
степенями свободы.
2) Пусть 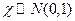 и независимы от
и независимы от 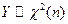 , тогда
, тогда
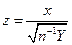
– распределение Стьюдента с 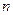 степенями свободы.
степенями свободы.
Пусть задано 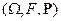 – полное вероятностное пространство. Пусть
– полное вероятностное пространство. Пусть 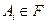 ;
; 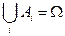 ,
, 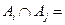 при
при 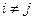 .
.
Определение. Случайную величину 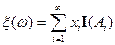 называют дискретной.
называют дискретной.
Если число слагаемых в 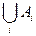 конечно, то
конечно, то  – простая случайная величина.
– простая случайная величина.
Теорема. 1) Для любой случайной величины 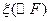 существует последовательность случайных величин
существует последовательность случайных величин 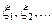 такая, что
такая, что  и
и
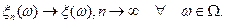
2) Если 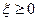 , то существует последовательность простых случайных величин
, то существует последовательность простых случайных величин 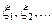 таких что
таких что
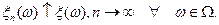
 2014-02-12
2014-02-12 1253
1253
