Задача о разорении.
Доказательство.
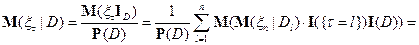
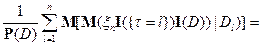
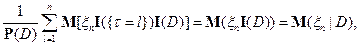
следовательно,
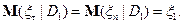
Теорема доказана.
Пусть 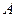 –количество денег 1-ого игрока,
–количество денег 1-ого игрока, 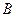 – количество денег 2-ого игрока. Введем последовательность
– количество денег 2-ого игрока. Введем последовательность 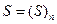 .
. 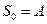 ;
; 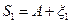 ;
;
 ;
; 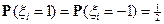 ;
; 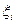 независимы.
независимы.
Обозначим момент разорения одного из игроков 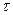 :
:
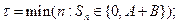
Поскольку 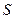 – мартингал
– мартингал 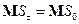 , т.е.
, т.е. 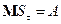 ;
;
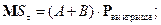
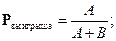
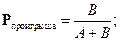
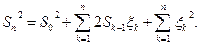
Так как
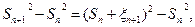
то
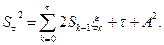
При этом 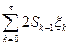 – мартингал, следовательно,
– мартингал, следовательно,
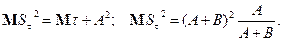
Таким образом среднее время игры равно 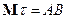 .
.
2. Некоторые задачи и определения математической статистики
Рассмотрим схему серий Бернулли 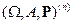 с
с
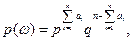
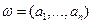 .
.
Пусть 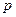 (и
(и 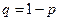 ) – неизвестны заранее, а наблюдаемы
) – неизвестны заранее, а наблюдаемы 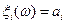 . Вместо
. Вместо 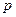 традиционно используется
традиционно используется 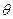 – неизвестный оцениваемый параметр. Возможны две постановки задачи:
– неизвестный оцениваемый параметр. Возможны две постановки задачи:
1) задача оценивания;
2) задача построения доверительных интервалов.
Пусть 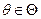 (здесь
(здесь 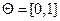 ).
).
Следовательно, задана статистическая модель 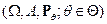 с
с
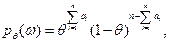
отвечающая 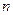 независимым испытаниям.
независимым испытаниям.
Всякую функцию 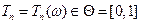 назовем оценкой.
назовем оценкой.
Определение. Оценка 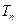 состоятельна, если
состоятельна, если
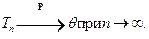
Определение. Оценка несмещенная, если
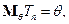
где 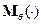 отвечает мере
отвечает мере 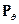 .
.
Определение. Оценка 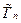 эффективна (в классе несмещенных оценок
эффективна (в классе несмещенных оценок 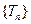 ), если
), если
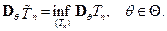
Пример. Если 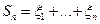 и
и 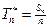 , то из закона больших чисел следует, что
, то из закона больших чисел следует, что
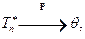
т.е. 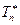 – состоятельная оценка в схеме Бернулли,
– состоятельная оценка в схеме Бернулли,
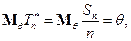
следовательно, 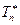 – несмещенная. Но любая оценка
– несмещенная. Но любая оценка
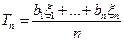
с 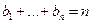 несмещенная, и при
несмещенная, и при 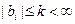 – состоятельная, а вот эффективна ли она? Ответ – в так называемом неравенстве Рао-Крамера.
– состоятельная, а вот эффективна ли она? Ответ – в так называемом неравенстве Рао-Крамера.
Теорема. Для несмещенных оценок 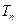 справедливо неравенство
справедливо неравенство
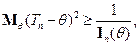
где 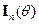 – информация Фишера.
– информация Фишера.
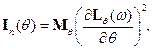
где 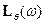 – функция правдоподобия (логарифмическая),
– функция правдоподобия (логарифмическая),
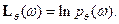
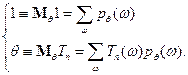
Продифференцируем по 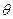 :
:
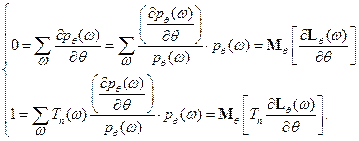
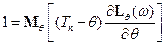
и, следовательно, по неравенству Коши-Буняковского
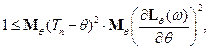
т.е.
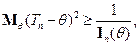
где
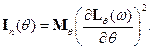
Неравенство доказано (в том числе для общей схемы, не обязательно для схемы Бернулли).
Покажем с помощью неравенства Рао-Крамера, что в схеме Бернулли 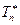 –эффективная оценка.
–эффективная оценка.
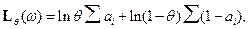
следовательно,
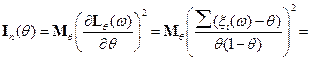
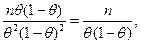
но
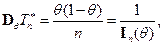
следовательно,
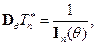
а для всякой другой 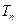
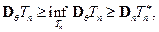
следовательно, 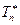 – эффективна.
– эффективна.
Из закона больших чисел при 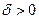

и, следовательно, для любого 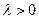
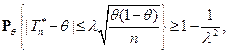
поэтому,
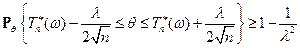
и, следовательно,
Определение. Интервал вида 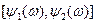 , где
, где 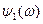 и
и 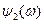 – две функции элементарных событий называется доверительным интервалом надежности
– две функции элементарных событий называется доверительным интервалом надежности 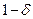 или доверительным интервалом с уровнем значимости
или доверительным интервалом с уровнем значимости 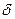 , если для любого
, если для любого 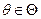
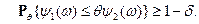
В примере имели место равенства
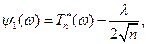
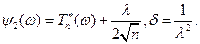
3. Вероятностная модель в общей постановке (в том числе с бесконечным числом исходов)
Ранее рассматривалось 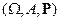 с
с 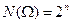 , а если
, а если 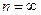 ? (Рассмотрите пример с интервалом [0,1)).
? (Рассмотрите пример с интервалом [0,1)).
Определение. Система 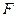 подмножеств
подмножеств 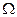 называется
называется 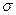 - алгеброй, если она является алгеброй и если
- алгеброй, если она является алгеброй и если 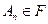 ,
, 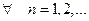 , то
, то
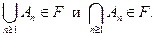
(Рассмотрите пример с борелевской 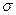 -алгеброй
-алгеброй 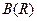 , пример с точечной
, пример с точечной 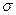 -алгеброй).
-алгеброй).
Определение. Вероятностной мерой или вероятностью на 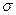 - алгебре
- алгебре 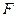 называется числовая функция множеств
называется числовая функция множеств 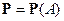 ,
, 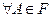 , если
, если
1) 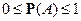 ;
;
2) 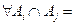 при
при 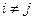 из
из 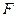
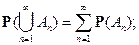
3) 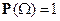 .
.
Определение. (Аксиоматика Колмогорова.) Набор 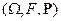 , где
, где
а) 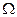 – множество
– множество 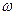 – пространство элементарных событий
– пространство элементарных событий
б) 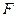 –
– 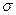 -алгебра подмножеств
-алгебра подмножеств 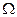 ;
; 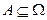 ,
, 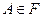
в) 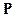 – вероятность на
– вероятность на 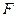
называется полным вероятностным пространством, а 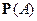 – вероятностью события
– вероятностью события 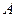 .
.
Определение. Случайная величина 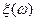 – это любая определенная на
– это любая определенная на 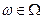 ,
, 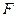 -измеримая числовая функция
-измеримая числовая функция 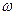 (т.е. для любого
(т.е. для любого 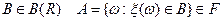 , где
, где 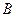 – из борелевской
– из борелевской 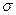 - алгебры
- алгебры 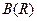 – на
– на 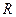 ).
).
Определение. Функцией распределения называется 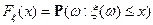 .
.
Функцией распределения может являться любая функция 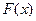 такая, что
такая, что
1) 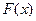 – неубывающая функция
– неубывающая функция
2) 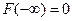 ,
,  , где
, где 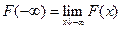 ;
; 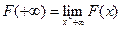
3) 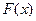 непрерывна справа, имеет предел слева
непрерывна справа, имеет предел слева 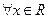 , т.е.
, т.е.
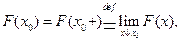
и 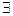
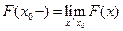 .Тогда
.Тогда
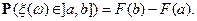
Примеры мер:
1) дискретных, с кусочно-постоянной функцией распределения 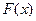
2) абсолютно-непрерывных с плотностью
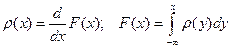
3) сингулярных.
Теорема Лебега.
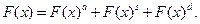
 2014-02-12
2014-02-12 631
631








