При решении многих практических задач приходится иметь дело с дискретными случайными величинами,
которые подчиняются закону распределения Пуассона. Типичными примерами случайной величины, имеющей
распределение Пуассона, являются: число вызовов на телефонной станции за некоторое время 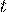 ; число
; число
отказов сложной аппаратуры за время 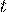 , если известно, что отказы независимы друг от друга и в среднем на
, если известно, что отказы независимы друг от друга и в среднем на
единицу времени приходится 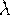 отказов.Ряд распределения будет иметь вид:
отказов.Ряд распределения будет иметь вид:
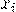 | ... | 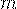 | ... | ||
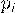 | 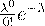 | 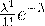 | ... | 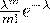 | ... |
То есть вероятность того, что случайная величина 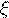 примет значение
примет значение 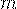 вычисляется по формуле Пуассона:
вычисляется по формуле Пуассона:
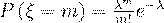
поэтому данный закон и называется законом распределения Пуассона.
Случайная величина, распределенной по закону Пуассона, имеет следующие числовые характеристики:
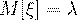 (44)
(44)
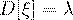 (45)
(45)
 (46)
(46)
Распределение Пуассона зависит от одного параметра 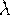 , который является математическим ожиданием
, который является математическим ожиданием
случайной величины. На рисунке 14 показан общий вид многоугольника распределения Пуассона при
различных значениях параметра 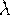 .
.
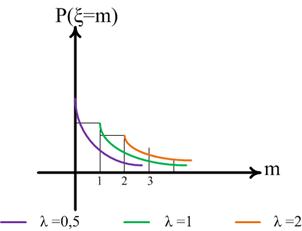
Рис.14
Распределение Пуассона может быть использовано как приближенное в тех случаях, когда точным
распределением случайной величины является биномиальное распределение, при этом число испытаний
велико, а вероятность появления события 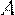 в отдельном испытании мала, поэтому закон распределения
в отдельном испытании мала, поэтому закон распределения
Пуассона называют законом редких событий. А еще, если математическое ожидание мало отличается от
дисперсии, то есть когда 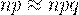 . В связи с этим распределение Пуассона имеет большое количество
. В связи с этим распределение Пуассона имеет большое количество
различных приложений.
Пример 16. Завод отправляет на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие
повредится, равна 0,002. Найти математическое ожидание числа поврежденных при перевозке деталей.
Решение. Случайная величина 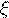 имеет распределение Пуассона, поэтому
имеет распределение Пуассона, поэтому 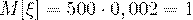 .
.
Вопрос. Вероятность искажения символа при передаче сообщения равна 0,004. Чтобы среднее число
искаженных символов было равно 4, надо передать 100 символов.
верно
неверно
 2014-02-12
2014-02-12 765
765








