Биномиальный закон распределения

Среди законов распределения для дискретных случайных величин наиболее распространенным является
биномиальный закон распределения. Биномиальное распределение имеет место в следующих условиях.
Пусть случайная величина 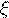- число появлений некоторого события 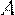в 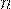независимых
испытаниях, вероятность появления 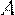в отдельном испытании равна 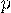. Данная случайная величина
является дискретной случайной величиной, ее возможные значения 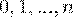. Вероятность того, что случайная величина 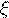примет значение 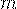вычисляется по формуле Бернулли: .

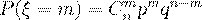Определение 15. Закон распределения дискретной случайной величины 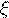называется биномиальным законом
распределения, если вероятности значений случайной величины вычисляются по формуле Бернулли.

Ряд распределения будет иметь вид:

			...
			...

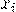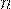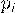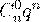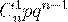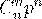Убедимся, что сумма вероятностей различных значений случайной величины равна 1. Действительно,

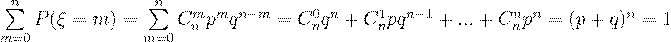
Так как при данных вычислениях получилась биномиальная формула Ньютона, поэтому закон распределения
называется биномиальным.
Если случайная величина 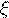имеет биномиальное распределение, то ее числовые характеристики находятся по
формулам:

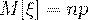(41)

(42)

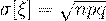(43)

Пример 15. Имеется партия из 50 деталей. Вероятность брака для одной детали 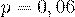. Пусть случайная
величина 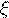- число бракованных деталей в данной партии. Найти математическое ожидание, дисперсию и
среднее квадратичное отклонение данной случайной величины.
Решение. Случайная величина 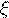имеет биномиальное распределение, так как вероятность того, что она примет значение 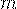вычисляется по формуле Бернулли. Тогда ее математическое ожидание находится по формуле (41), а именно, 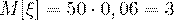; дисперсию находим по формуле (42): .
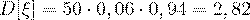Тогда среднее квадратичное отклонение будет равно .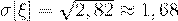

Вопрос. Приобретено 200 лотерейных билетов, вероятность выигрыша одного билета равна 0,01. Тогда среднее число лотерейных билетов, на которые выпадут выигрыши, равно:
а) 10;
б) 2;
в) 20;
г) 1.

в)

а)

г)

б)