Определение 16. Непрерывная случайная величина 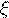 имеет равномерное распределение на отрезке [a;b],
имеет равномерное распределение на отрезке [a;b],
если на этом отрезке плотность распределения данной случайной величины постоянна, а вне его равна нулю,
то есть
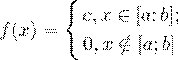 (45)
(45)
График плотности для равномерного распределения изображен на рисунке 15:
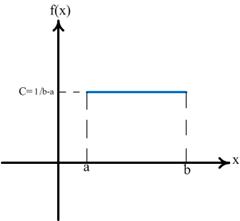
Рис.15
Так как площадь под кривой распределения должна равняться 1, то 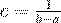 и следовательно,
и следовательно,
плотность распределения имеет вид:
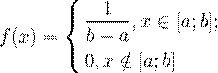 (46)
(46)
Непрерывная случайная величина 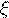 подчиняется закону равномерного распределения, если ее возможные
подчиняется закону равномерного распределения, если ее возможные
значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все
значения случайной величины одинаково вероятны. Случайные величины, имеющие равномерное
распределение часто встречаются в измерительной практике при округлении отсчетов измерительных
приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является
случайной величиной 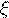 , которая может принимать с постоянной плотностью вероятности любое значение
, которая может принимать с постоянной плотностью вероятности любое значение
между двумя соседними целыми делениями.
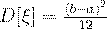
Числовые характеристики случайной величины, имеющей равномерное распределение, вычисляются по формулам:
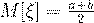 (47)
(47)
 (48)
(48)
 (49)
(49)
Функция распределения вероятностей случайной величины, равномерно распределенной на промежутке 
имеет вид:
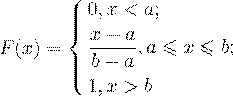 (50)
(50)
График данной функции представлен на рисунке 16:
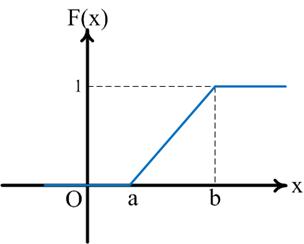
Рис.16
Пример 17. Цена деления шкалы измерительного прибора равна 0,1. Показания прибора округляют до
ближайшего деления. Найти математическое ожидание случайной величины 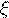 - ошибки округления.
- ошибки округления.
Решение. Случайная величина 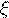 - ошибка округления имеет равномерное распределение на промежутке
- ошибка округления имеет равномерное распределение на промежутке
от 0 до 0,1, ее математическое ожидание вычисляется по формуле (47): 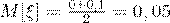 .
.
Вопрос. Непрерывная случайная величина 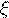 имеет плотность распределения вероятностей
имеет плотность распределения вероятностей
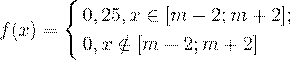
Тогда ее дисперсия равна:
а)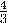 ;
;
б)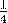 ;
;
в)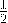 ;
;
г)  .
.
г)
а)
в)
б)
Среди распределений непрерывных случайных величин центральное место занимает нормальный закон,
плотность распределения которого имеет вид:
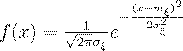 (51)
(51)
где 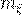 - математическое ожидание, а
- математическое ожидание, а 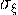 - среднее квадратичное отклонение данной случайной
- среднее квадратичное отклонение данной случайной
величины.
График плотности распределения нормального закона называют кривой Гаусса, он приведен на рисунке 17:
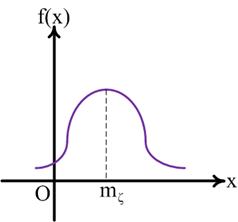
Рис.17
Отметим некоторые свойства кривой Гаусса.
1. Кривая распределения симметрична относительно ординаты, проходящей через точку 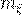 .
.
2. Кривая имеет один максимум при 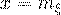 , равный
, равный 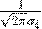 .
.
3. При 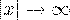 ветви кривой асимптотически приближаются к оси
ветви кривой асимптотически приближаются к оси 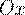 .
.
4. Изменение математического ожидания 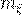 при
при  приводит к смещению кривой
приводит к смещению кривой
распределения вдоль оси 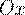 . При этом кривая распределения сохраняет свой вид.
. При этом кривая распределения сохраняет свой вид.
При изменении среднего квадратичного отклонения при 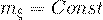 кривая распределения изменяет свой вид.
кривая распределения изменяет свой вид.
На рисунке 18 показана зависимость кривой распределения от среднего квадратичного отклонения.
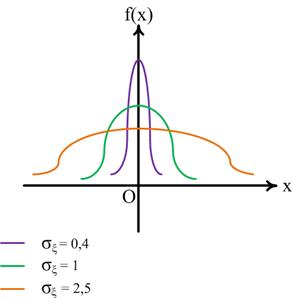
Рис.18
Функция распределения вероятностей для нормального закона имеет вид:
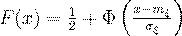 (52)
(52)
где 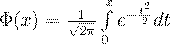 - функция Лапласа.
- функция Лапласа.
Нормальный закон распределения очень широко распространен в задачах практики. Он проявляется во всех тех
случаях, когда случайная величина 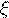 является результатом действия большого числа различных факторов.
является результатом действия большого числа различных факторов.
Каждый фактор в отдельности на величину 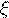 влияет незначительно и нельзя указать, какой именно в большей
влияет незначительно и нельзя указать, какой именно в большей
степени, чем остальные. Примерами случайных величин, имеющих нормальное распределение, могут служить:
отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров; ошибки при
измерении; отклонения при стрельбе и другие.
Основной особенностью, выделяющей нормальный закон среди других законов, служит то, что он является
предельным законом для других законов распределения.
Вероятность того, что случайная величина 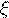 , распределенная по нормальному закону, попадет на промежуток
, распределенная по нормальному закону, попадет на промежуток
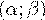 вычисляется по формуле:
вычисляется по формуле:
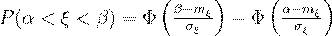 (53)
(53)
Вероятность того, что случайная величина 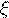 отклонится от своего математического ожидания на величину по
отклонится от своего математического ожидания на величину по
модулю меньшую 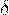 вычисляется по формуле:
вычисляется по формуле:
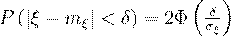 (54)
(54)
Пример18. Ошибка радиодальномера подчинена нормальному закону. Математическое ожидание этой ошибки
равно 5 м, а среднее квадратичное отклонение равно 10 м. Найти вероятность того, что измеренное значение
дальности будет отклоняться от истинного не более чем на 20 м.
Решение. По условию надо найти вероятность попадания случайной величины 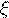 - ошибки радиодальномера
- ошибки радиодальномера
на промежуток 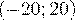 . По формуле (53) находим:
. По формуле (53) находим:
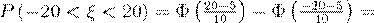
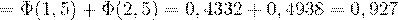 .
.
Вопрос. Нормальное распределение характеризуется одним параметром.
неверно
верно
 2014-02-12
2014-02-12 3190
3190