Пусть в n-мерном линейном пространстве Rnимеются два базиса: 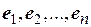 (старый) и
(старый) и 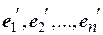 (новый). Каждый вектор пространства Rnможет быть представлен в виде линейной комбинации базисных векторов. Предположим, что векторы
(новый). Каждый вектор пространства Rnможет быть представлен в виде линейной комбинации базисных векторов. Предположим, что векторы 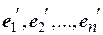 выражаются через базисные векторы
выражаются через базисные векторы 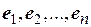 с помощью формул
с помощью формул
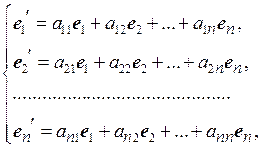 (4.1)
(4.1)
Матрицу
А = 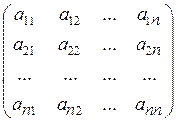
называют матрицей перехода от старого базиса к новому.
Определитель матрицы А отличен от нуля, так как иначе в силу теоремы 3.7 строки этой матрицы (а значит, и базисные векторы 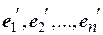 ) оказались бы линейно зависимыми.
) оказались бы линейно зависимыми.
Докажем, что обратный переход от нового базиса 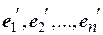 к старому базису
к старому базису 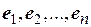 осуществляется с помощью матрицы В, обратной к матрице А.
осуществляется с помощью матрицы В, обратной к матрице А.
По теореме 3.8 матрица В, обратная к матрице А, имеет вид
В = 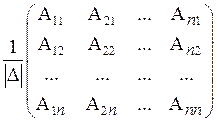 , (4.2)
, (4.2)
где через 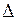 обозначен определитель матрицы А, а через
обозначен определитель матрицы А, а через 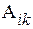 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 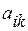 матрицы А.
матрицы А.
Умножим уравнения (4.1) соответственно на алгебраические дополнения 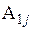 ,
, 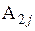 ,…,
,…,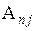 элементов j -го столбца определителя
элементов j -го столбца определителя 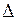 и после этого сложим эти уравнения. В результате получим (для любого номера j, равного 1,2,…, n)
и после этого сложим эти уравнения. В результате получим (для любого номера j, равного 1,2,…, n)
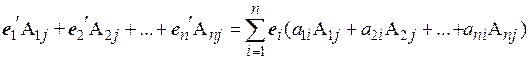 (4.3)
(4.3)
Сумма произведений элементов i -го столбца на соответствующие алгебраические дополнения элементов j -го столбца определителя 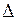 равна нулю при
равна нулю при 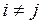 (теорема 3.5), если же
(теорема 3.5), если же 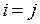 , то эта сумма представляет собой разложение определителя
, то эта сумма представляет собой разложение определителя 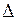 по элементам j -го столбца (теорема 3.4). Тогда
по элементам j -го столбца (теорема 3.4). Тогда
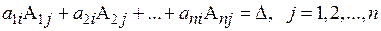 .
.
Равенства (4.3) запишутся в виде
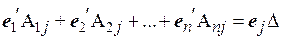 ,
,
откуда 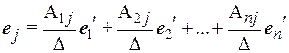 ,
, 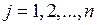 , или
, или
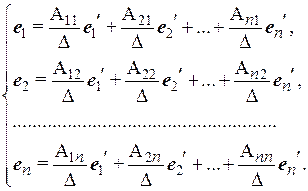 (4.4)
(4.4)
Формулы (4.4) показывают, что обратный переход от базиса 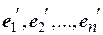 к базису
к базису 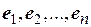 осуществляется с помощью
осуществляется с помощью
матрицы В = А–1.
Найдем зависимость между координатами вектора в разных базисах. Пусть х – произвольный вектор рассматриваемого пространства Rn; (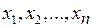 ) – его координаты в старом базисе
) – его координаты в старом базисе 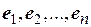 , (
, (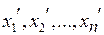 )– его координаты в новом базисе
)– его координаты в новом базисе 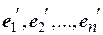 , так что
, так что
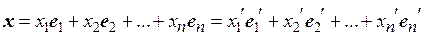 . (4.5)
. (4.5)
Подставив в правую часть равенства (4.5) вместо векторов 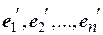 их выражения, определяемые формулами (4.1), получим
их выражения, определяемые формулами (4.1), получим
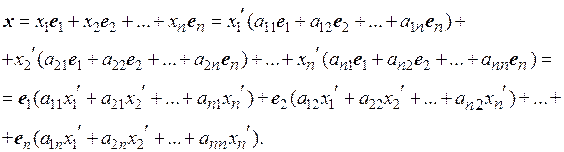
Из последнего равенства в силу единственности разложения по базису 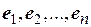 получаем формулы перехода от координат
получаем формулы перехода от координат 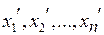 в новом базисе к координатам
в новом базисе к координатам 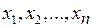 в старом базисе:
в старом базисе:
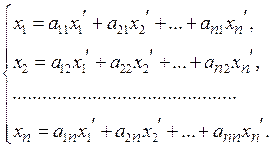 (4.6)
(4.6)
Равенства (4.6) можно представить в матричной форме
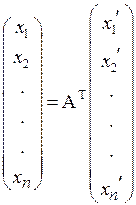 или
или 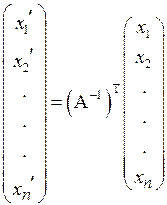 , (4.7)
, (4.7)
где АТ и (А–1)Т– матрицы, транспонированные по отношению к матрице А и обратной матрице АТ, соответственно.
Пример. В базисе 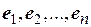 заданы векторы
заданы векторы 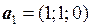 ,
, 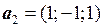 ,
, 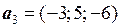 и
и 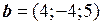 . Показать, что векторы
. Показать, что векторы 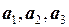 образуют базис и выразить вектор b в базисе
образуют базис и выразить вектор b в базисе 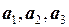 .
.
○ Три трехмерных вектора образуют базис, если они линейно независимы. Чтобы доказать линейную независимость векторов 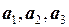 , вычислим определитель, составленный из координат этих векторов:
, вычислим определитель, составленный из координат этих векторов:
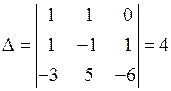 .
.
Определитель не равен нулю, значит, векторы 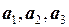 линейно независимы и образуют базис. Выразим связь между базисами:
линейно независимы и образуют базис. Выразим связь между базисами:
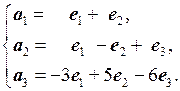
Матрица перехода от базиса  к базису
к базису  имеет вид
имеет вид
А= 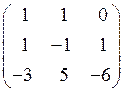 .
.
Вычисляем обратную матрицу А–1 по формуле (4.2) и находим транспонированную матрицу (А–1)Т:
А–1=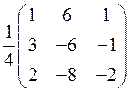 ; (А–1)Т=
; (А–1)Т= 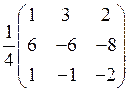 .
.
Теперь по формуле (4.7) находим координаты вектора b:
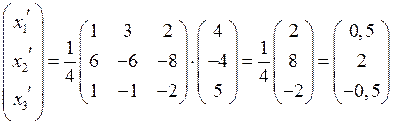 .
.
Таким образом, координаты вектора b в базисе  есть (0,5;2;–0,5) и вектор b может быть представлен в виде:
есть (0,5;2;–0,5) и вектор b может быть представлен в виде:
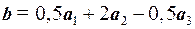 . ●
. ●
 2014-02-12
2014-02-12 11527
11527
