Условие совместности системы линейных уравнений

Установим необходимое и достаточное условие совместности системы (5.1).

Теорема 5.1. (теорема Кронекера-Капелли). Для того чтобы система линейных уравнений являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.

□ 1) Необходимость. Пусть система уравнений (5.1) совместна, то есть имеет решение 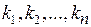. Тогда 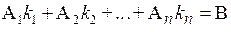– верное векторное равенство, то есть вектор-столбец В свободных членов системы является линейной комбинацией вектор-столбцов 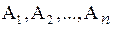. Пусть ранг матрицы А системы равен r. Расширенная матрица 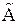системы получается из матрицы А добавлением столбца В. Но по свойству 1 ранга матрицы, добавление столбца, являющегося линейной комбинацией других столбцов матрицы не изменяет ранга матрицы. Значит ранг расширенной матрицы 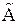также равен r,
т.е. r (A) = r (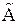). Необходимость доказана.

2) Достаточность. Пусть ранги основной и расширенной матриц системы (1) равны: r (A) = r (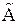) = r. Тогда r базисных столбцов
матрицы А являются базисными столбцами и расширенной матрицы 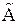, и любой (r +1)-й столбец матрицы 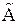будет линейной комбинацией
этих r столбцов. Пусть для определенности базисными будут первые r столбцов 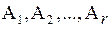(этого всегда можно достичь, поменяв местами соответствующие столбцы, что не изменит ранга матрицы). Значит, столбец В матрицы 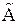представляет собой некоторую линейную комбинацию столбцов 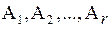, т.е. 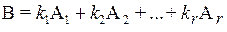, или 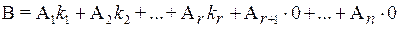– верное векторное равенство. Это означает, что совокупность n чисел (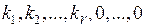) является решением системы (5.1). Теорема полностью доказана. ■

Теорема Кронекера-Капелли устанавливает необходимое и достаточное условие совместности системы линейных уравнений, но не дает способа нахождения решений этой системы.