В задачах, рассматриваемых в теоретической механике, нет необходимости учитывать ненормированность векторов базиса криволинейных систем координат, поскольку вектора, составляющие эти базисы, всегда можно сделать нормированными на единицу. Однако остается проблема корректного учета вращения координатного базиса одной системы координат относительно координатного базиса другой системы координат. Такая проблема возникает, например, при переходе из декартовой системы координат в цилиндрическую или сферическую системы координат. Рассмотрим подобную ситуацию подробнее.
Положим, что координатный базис 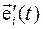 вращается относительно неподвижного координатного базиса
вращается относительно неподвижного координатного базиса 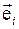 . Рассмотрим произвольный вектор
. Рассмотрим произвольный вектор 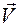 . В обеих системах координат этот вектор имеет представление:
. В обеих системах координат этот вектор имеет представление:
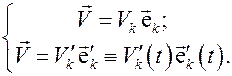
Зависимость от времени в представлении вектора 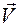 в базисе
в базисе 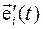 возникает вследствие подвижности этого базиса. Поскольку в дальнейших рассуждениях мы будем полагать ортонормированность обоих координатных базисов
возникает вследствие подвижности этого базиса. Поскольку в дальнейших рассуждениях мы будем полагать ортонормированность обоих координатных базисов
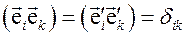 ,
,
ковариантные и контравариантные компоненты вектора будут совпадать. При преобразовании систем координат компоненты вектора 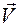 в различных системах будут связаны преобразованием
в различных системах будут связаны преобразованием
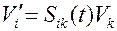
Подставим выражение (3.2) в разложение вектора 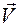 по подвижному реперу
по подвижному реперу
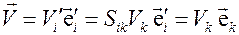 ,
,
где 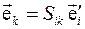 , или
, или 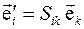 . Следовательно, матрица
. Следовательно, матрица 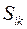 определяет ориентацию векторов координатного базиса
определяет ориентацию векторов координатного базиса 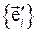 относительно векторов координатного базиса
относительно векторов координатного базиса 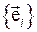 . Найдем элементы
. Найдем элементы 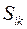 .
.
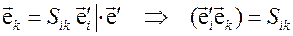
Таким образом, элементы матрицы, описывающей переход из неподвижного репера в подвижный равны проекциям соответствующих векторов подвижного репера на вектора неподвижного репера (в силу ортонормированности обоих реперов 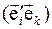 - направляющие косинусы).
- направляющие косинусы). 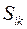 - к-я компонента вектора
- к-я компонента вектора 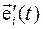 в неподвижной системе координат.
в неподвижной системе координат.
Исследуем свойства матрицы 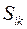 . Для этого рассмотрим скалярное произведение
. Для этого рассмотрим скалярное произведение
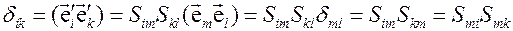
или,
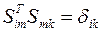
Откуда следует, что обратная матрица совпадает с транспонированной матрицей  . Заметим, что матрица
. Заметим, что матрица 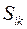 , в силу независимости длины вектора
, в силу независимости длины вектора 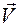 от выбора системы координат, является унимодулярной.
от выбора системы координат, является унимодулярной.
Обратимся теперь к последовательному описанию вращения подвижного репера.
Запишем соотношение, обратное соотношению (5.3)
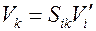 .
.
Положим, что вектор 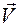 постоянен в координатном базисе
постоянен в координатном базисе 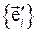 , или другими словами, вращается вместе с подвижным координатным базисом. Тогда, дифференцируя по времени соотношение (5.8) и используя соотношение (5.3), получаем
, или другими словами, вращается вместе с подвижным координатным базисом. Тогда, дифференцируя по времени соотношение (5.8) и используя соотношение (5.3), получаем
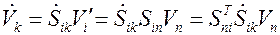 .
.
Введем обозначение
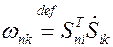 ,
,
где 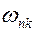 является тензором второго ранга. Этот тензор называется тензором угловой скорости. И теперь
является тензором второго ранга. Этот тензор называется тензором угловой скорости. И теперь
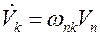
Выясним свойства тензора угловой скорости. Для этого обратимся к условию ортогональности матрицы 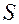 (5.7). Дифференцируя это соотношение по времени, получаем
(5.7). Дифференцируя это соотношение по времени, получаем
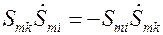 .
.
Откуда, согласно определению тензора угловой скорости (5.9), получаем
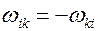 .
.
Следовательно, тензор угловой скорости является антисимметричным тензором второго ранга. Отсюда следует, что этот тензор имеет только три независимые компоненты и, следовательно, он дуален вектору угловой скорости. Определим компоненты вектора угловой скорости по правилу
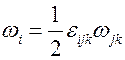 ,
,
где 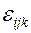 - полностью антисимметричный символ Леви – Чивитта. Подставляя (5.12) определение тензора угловой скорости (5.9) найдем компоненты вектора угловой скорости
- полностью антисимметричный символ Леви – Чивитта. Подставляя (5.12) определение тензора угловой скорости (5.9) найдем компоненты вектора угловой скорости
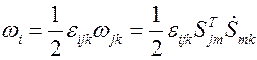 .
.
Вернемся к определению вектора угловой скорости (5.12). Свернем его с символом Леви – Чивитта
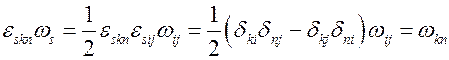 .
.
Следовательно,
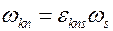 .
.
Вернемся к соотношению (5.10). Подставляя в него связь между вектором и тензором угловой скорости (5.14) получаем
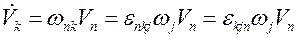 ,
,
или в векторной форме
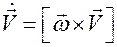
Мы получили правило дифференцирования произвольного вектора, вращающегося вместе с координатным репером относительно неподвижного координатного репера.
Заметим, что 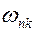 и
и 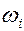 компоненты тензора и вектора угловой скорости, заданные в неподвижном координатном базисе
компоненты тензора и вектора угловой скорости, заданные в неподвижном координатном базисе 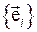 . Рассмотрим описание этих величин в подвижном базисе. Для этого рассмотрим закон преобразования тензора угловой скорости при переходе из неподвижного координатного базиса в подвижный
. Рассмотрим описание этих величин в подвижном базисе. Для этого рассмотрим закон преобразования тензора угловой скорости при переходе из неподвижного координатного базиса в подвижный
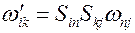 .
.
Подставляя в выражение (5.16) определение тензора угловой скорости (5.9) получим выражение тензора угловой скорости в подвижном координатном базисе
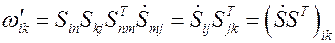
Повторяя все рассуждения, проведенные выше, нетрудно, опираясь на выражение (5.17), получить связь между вектором угловой скорости в подвижном координатном базисе и матрицей преобразования 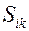

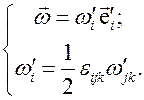
Рассмотрим пример преобразования неподвижного координатного репера в подвижный репер. Найдем выражения для скорости и ускорения материальной точки в цилиндрических координатах.
Обратимся к рисунку 1, на котором изображены координатные базисы неподвижной (декартовой) системы координат 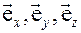 и подвижной (цилиндрической) системы координат
и подвижной (цилиндрической) системы координат 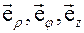 . Напомним, что закон преобразования декартовых координат в цилиндрические имеет вид
. Напомним, что закон преобразования декартовых координат в цилиндрические имеет вид
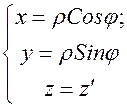 .
.
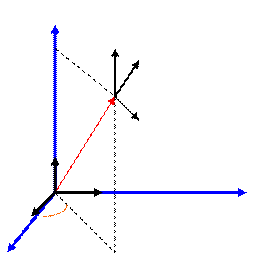
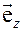
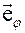
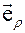
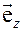
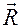
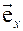
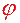
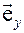
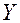
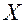
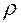
Рис. 1.
1. Используя соотношение (5.5) строим матрицу преобразования декартовых координат в цилиндрические, проектируя соответствующим образом орты цилиндрического базиса на орты декартового базиса. В результате мы получаем матрицу 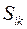 , описывающую переход из декартовой системы координат в цилиндрическую систему координат, в виде.
, описывающую переход из декартовой системы координат в цилиндрическую систему координат, в виде.
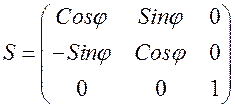
2. Используя выражение (5.17) 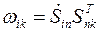 , находим тензор угловой скорости
, находим тензор угловой скорости
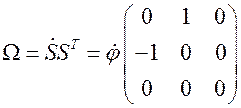 (5.21)
(5.21)
3. Согласно выражению (5.18) вычисляем компоненты угловой скорости:
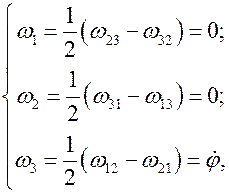 (5.22)
(5.22)
следовательно, вектор угловой скорости вращения репера цилиндрической системы координат направлен вдоль оси 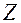 и имеет вид
и имеет вид
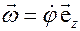 . (5.23)
. (5.23)
4. Воспользуемся общим правилом дифференцирования ортов подвижного репера (5.15). Используя выражение для угловой скорости (5.20), находим производные от ортов цилиндрической системы координат:
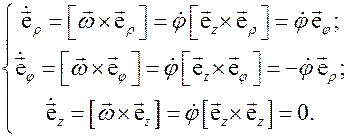 (5.24)
(5.24)
5. Запишем разложение радиус – вектора  материальной точки (Рис.1) по цилиндрическому базису
материальной точки (Рис.1) по цилиндрическому базису 
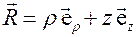 .
.
6. Дифференцируя по времени это разложение, и подставляя полученные выше соотношения (5.21), получим выражения для скорости и ускорения материальной точки в цилиндрических координатах:
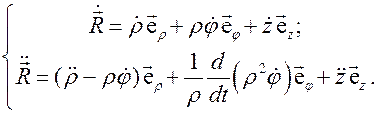
Задание для самостоятельного решения:
1. Найти скорость и ускорение материальной точки в сферических координатах.
 2015-07-04
2015-07-04 2074
2074
