Задание 34. Преобразования графиков функций – 3 ч

Цель: формирование умения строить графики функций методом преобразований: параллельного переноса, растяжения и сжатия вдоль осей координат, симметрии относительно оси Ох.

Задание для самостоятельной внеаудиторной работы:

& 34.1.Разберите, какие преобразования графиков функции возможны.

Основные сведения из теории:

34.2. Заполните пропуски:

Сдвиг графика функции задаётся преобразованиями вида:

· вдоль оси Ох: …

· вдоль оси Оу: …

Растяжение графика функции задаётся преобразованиями вида:

· вдоль оси Ох: …

· вдоль оси Оу: …

Сжатие графика функции задаётся преобразованиями вида:

· вдоль оси Ох: …

· вдоль оси Оу: …

Отражение графика функции относительно оси Ох задаётся преобразованиями вида: …

Отражение части графика функции, расположенной ниже оси Ох, относительно оси Ох задаётся преобразованиями вида: …

Примеры и упражнения:

?34.3. Постройте на одном чертеже графики функций методом преобразований:

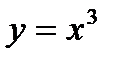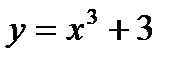а) ; б) ; в) .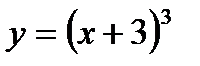

?34.4. Постройте график функции методом преобразований:

а) 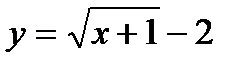; б) .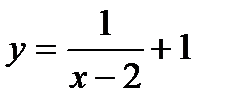

Укажите область определения и область значения функции.

?34.5. Постройте на одном чертеже графики функций методом преобразований:

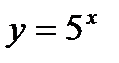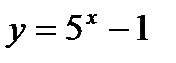а) ; б) ; в) .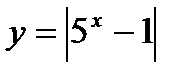

?34.6. Постройте график функции методом преобразований:

а) 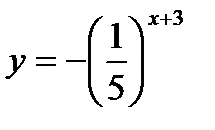; б) .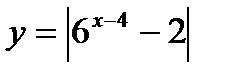

Укажите область определения и область значения функции.

?34.7. Постройте на одном чертеже графики функций методом преобразований:

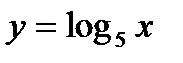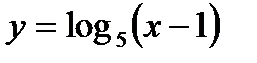а) ; б) ; в) .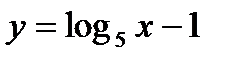

?34.8. Постройте график функции методом преобразований:

а) 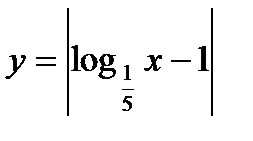; б) .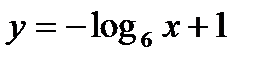

?34.9. Постройте на одном чертеже графики функций методом преобразований:

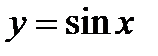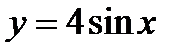а) ; б) ; в) .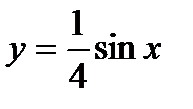

Укажите область значения функций.

?34.10. Постройте график функции методом преобразований:

а) 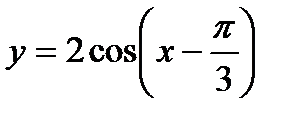; б) .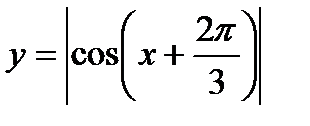

?34.11. Постройте на одном чертеже графики функций методом преобразований:

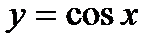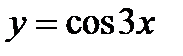а) ; б) ; в) .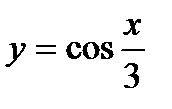

Укажите период данных функций.

?34.12. Постройте график функции методом преобразований:

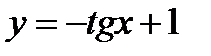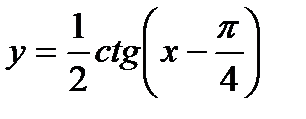а) ; б) ; ¶в)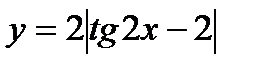

Список литературы:

1. Сайт для подготовки к ЕГЭ по математике: http://uztest.ru/abstracts/?id=51&t=3.