Свойства решений однородной системы уравнений

1°. Если К₁ и К₂ – решения однородной системы (5.18), то К₁ + К₂ является решением этой системы.

□ Действительно, по условию АК₁ = 0 и АК₂ = 0. Отсюда следует, что А(К₁+К₂) = АК₁+АК₂ = 0+0 = 0. ■

2°. Если К – решение однородной системы, то lК также решение этой системы, где l – произвольное число.

□ Так как АК=0, то А(lК)= l(АК)= l×0=0. ■

Из этих свойств следует, что любая линейная комбинация решений однородной системы линейных уравнений является решением этой системы. Поэтому естественно попытаться найти такие линейно независимые решения однородной системы, по которым разлагаются все ее решения.

Линейно независимые решения F₁, F₂, …, F _k однородной системы уравнений называются фундаментальной системой решений, если каждое решение системы уравнений является линейной комбинацией решений F₁, F₂, …, F _k.

Примем без доказательства следующую теорему.

Теорема 5.6. Однородная система линейных уравнений (5.21) 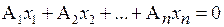, ранг r основной матрицы которой меньше числа неизвестных, т.е. 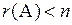, обладает фундаментальной системой решений, которая содержит 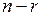решений.

Для построения фундаментальной системы решений нужно
найти любую совокупность 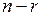линейно независимых решений системы (5.21).

Однородная система линейных уравнений всегда имеет нулевое решение, поэтому совместна. Так как по условию теоремы 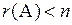, то система неопределенная и содержит 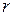базисных неизвестных. Пусть, для определенности, 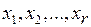– базисные неизвестные. Тогда 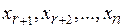– свободные неизвестные. Рассмотрим 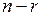наборов значений для свободных неизвестных, в каждом из которых только одному неизвестному придается значение 1, а остальные неизвестные полагаются равными нулю:

,

,

………………………….

.

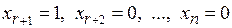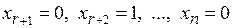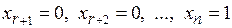Каждый такой набор свободных неизвестных определяет единственное решение системы (5.21):

F₁ = ,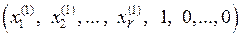

F₂ = ,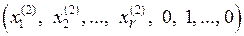

………………………………

= .

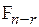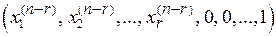Докажем, что F₁, F₂, …, F _n–r является линейно независимой системой решений системы уравнений (5.21). Для этого надо доказать, что векторное равенство

l₁F₁+ l₂F₂+ …+ l _n–r F _n–r = 0 (5.22)

выполняется только когда все коэффициенты l _i = 0, .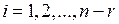

Векторное равенство (5.22) равносильно системе 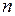уравнений относительно l₁, l₂, …, l _n–r:

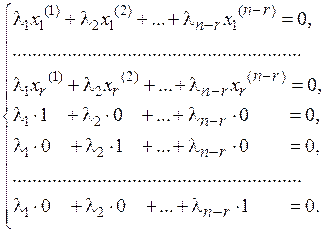(5.23)

Из последнего уравнения этой системы получим l _n–r = 0, из предпоследнего – l _{n–r– 1}=0, …, из (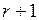)-го уравнения – l₁ = 0. Таким образом, система (5.23), а значит, и векторное уравнение (5.22), имеет единственное решение l _I = 0, 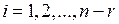. Отсюда следует линейная независимость совокупности решений F₁,F₂,…,F _n–r, которые и образуют фундаментальную систему решений системы (5.21).

Пример. Найти фундаментальную систему решений однородной

системы уравнений

○ Приведем к ступенчатому виду матрицу системы. Столбец свободных членов можно не записывать, так как при преобразованиях он не изменится.

~ ~ ~

~.

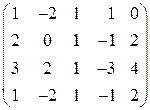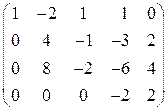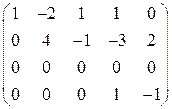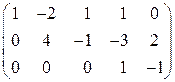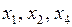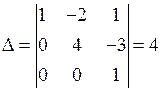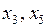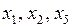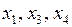Ранг матрицы системы равен 3, число неизвестных 4. В качестве базисных неизвестных можно взять , так как определитель матрицы из коэффициентов при этих неизвестных отличен от нуля. Тогда – свободные неизвестные. (За базисные неизвестные можно было также взять или , или 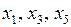). Выпишем полученную систему уравнений:

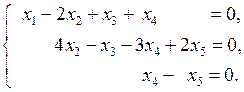(5.23)

Так как 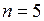, , 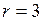то фундаментальная система решений будет состоять из двух векторов. Рассмотрим два набора значений свободных неизвестных:

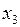= 1; ;

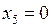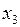= 0; .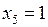

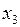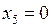Подставляя значения свободных неизвестных = 1; в
систему (5.23), найдем соответствующие значения главных неизвестных 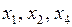и получим первое решение F₁=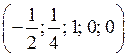. Подставляя
в общее решение (5.23) значения свободных неизвестных 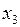= 0; 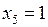, получим решение F₂=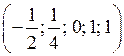. Решения F₁, F₂ образуют фундаментальную систему решений данной однородной системы. ●