Методы изучения связи социально-экономических явлений

Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных рядов, балансовый, аналитических группировок, графический, корреляции.

Метод параллельных рядов основан на сопоставлении двух или нескольких рядов статистических величин (табл. 21).

Таблица 21

Заводы Показатели
Производство
Себестоимость	7,6	8,0	9,0	9,5	10,0

Как видим, имеется следующая зависимость: чем меньше производство, тем выше себестоимость. Связь – обратная.

Балансовый метод основан на балансовом уравнении:

Он + П = В + Ок, где

Он – остатки на начало;

П – поступление;

В – выбытие;

Ок – остаток на конец.

Метод аналитических группировок является методом средних и относительных величин. Единицы совокупности группируются по факторному признаку, затем определяется средняя по результативному признаку, и их сравнивают для установления связи.

Графическая взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – результативного.

Корреляция – статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Существуют следующие варианты зависимостей:

· полная корреляция – связь между двумя признаками;

· частная корреляция – зависимость между результативным и одним из факторных признаков при фиксированном значении других факторных признаков;

· множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ – имеет своей задачей количественное определение тесноты связи между двумя признаками и между результативным и множеством факторных признаков. Количественное выражение тесноты связи называется коэффициентом корреляции.

Корреляция и регрессия тесно связаны между собой: корреляция оценивает силу (тесноту) связи, а регрессия исследует ее форму.

Корреляционно-регрессионный анализ включает в себя измерение тесноты, направления связи и формы связи.

Регрессионный анализ определяет связи, в которых изменение одной величины (результативный признак) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения.

Особую трудность для усвоения представляет корреляционный метод анализа взаимосвязи экономических явлений. Его проводят в три этапа: на первом осуществляется выбор формы связи между факторными и результативными признаками, т.е. выбирается тип аналитической функции; на втором осуществляется решение аналитического уравнения связи путем нахождения его параметров; на третьем определяется теснота связи между изучаемыми экономическими явлениями.

Прежде чем подробно остановится на каждом из трех этапов корреляционного анализа, обратим внимание на следующее.

В том случае, когда определяется влияние одного фактора на результативный признак, строится однофакторная регрессионная модель (парное управление корреляции); когда определяется влияние двух и более факторов на результативный признак, строится многофакторная регрессионная модель (уравнение множественной корреляции).

При подборе факторов для регрессионной модели следует помнить, что они не должны находится в функциональной связи с результативным признаком. В противном случае должен применяться индексный метод анализа, а не корреляционный. Следует также знать, что число наблюдений для построения однофакторной регрессионной модели должно быть 10-12.

Первый этап корреляционного анализа. Для определения формы связи между факторным и результативным признаками, т.е. для установления типа аналитической функции связи, применяют различные статистические методы, о которых уже шла речь. Чаще всего для установления формы зависимости между факторным и результативным признаками применяют графический метод.

При прямолинейной форме зависимости между факторным и результативным признаками функция связи имеет вид прямой: ŷ_x = α₀ + α₁x;

при параболической – вид параболы: ŷ_x = α₀ + α₁x + α₂x²

при гиперболической – вид гиперболы: ŷ_x = α_{0 + .}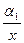

На втором этапе корреляционного анализа осуществляют решение аналитического уравнения связи путем нахождения его параметров α₀, α₁ …. α_n.

Параметр α₀ означает влияние на результативный признак не включенных в регрессионную модель факторов. Как правило, экономической интерпретации параметр α₀ не подлежит. Параметры α₁ …. α_n – коэффициенты регрессии – означают величину результативного признака при изменении факторного признака на единицу измерения.

В случае прямолинейной формы зависимости параметры аналитического уравнения связи ŷ_x = α₀ + α₁x находятся путем решения следующей системы уравнений:

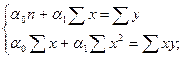
В случае параболической формы зависимости параметры аналитического уравнения связи ŷ_x = α₀ + α₁x + α₂x² находятся путем решения следующей системы уравнений:

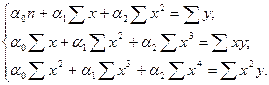
В случае гиперболической формы зависимости параметры аналитического уравнения связи ŷ_x = α_{0 +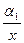} находятся путем решения следующей системы уравнений:

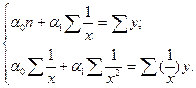
Для экономической интерпретации аналитического уравнения связи можно воспользоваться также коэффициентом эластичности, который рассчитывается по формуле:

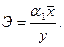
Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак при изменении факторного на 1 %.

На третьем этапе корреляционного анализа осуществляют оценку тесноты связи между факторным и результативным признаками с помощью показателей тесноты связи.

В случае линейной связи между факторным и результативным признаками производят расчеты линейного коэффициента корреляции по формуле:

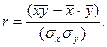
Линейный коэффициент корреляции варьируется в пределах от -1 до +1. Положительное его значение говорит о прямой связи, отрицательное – об обратной. Близость к нулю говорит о слабой связи, близость к ± 1 говорит о существенной связи, при r = ±1 – связь функциональная.

Таблица 22

Величина коэффициента корреляции	Характер связи
До ± 0,3	практически отсутствует
± 0,3 - ± 0,5	слабая
±0,5 - ±0,7	умеренная
±0,7 - ±1,0	сильная

В случае криволинейной зависимости (параболической, гиперболической) тесноту связи между факторным и результативным признакам определяют с помощью корреляционного отношения по формуле:

№ п/п рабочего	Стаж*, лет (x)	Разряд (y)	xy	x2	y2	ŷx
						2,4 3,1 3,1 3,4 3,4 4,1 4,3 4,6 5,0 5,1 5,2 6,3
Итого

Рассмотрим на конкретном примере применение корреляционного метода в изучении взаимосвязи экономических явлений. По данным таблицы 23 построим аналитическое уравнение связи и определим тесноту связи между явлениями.

Таблица 23

№ п/п рабочего

Разряд (y)

Стаж работы, лет (x)

Определим форму зависимости разряда рабочих от стажа их работы на предприятии, используя графический метод (рис.2).

Рис.2 Зависимость разряда рабочих от стажа их работы.

Судя по распределению, зависимость прямолинейная. Как известно, прямолинейная зависимость подчиняется уравнению прямой: ŷ_x = α₀ + α₁x. Следовательно, параметры данного уравнения связи находятся путем решения следующей системы уравнений:

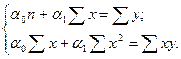
Для решения системы построим вспомогательную таблицу (табл. 24).

Таблица 24

· В ранжированном порядке (в порядке возрастания значений x)

На основе данных табл. 11.4 построим систему уравнений в следующем виде:

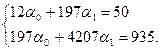
Решим эту систему:

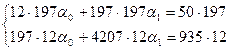
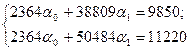
-11675а₁=1370

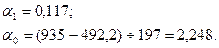
Следовательно, найденное аналитическое уравнение связи имеет вид: ŷ_x=2,248 + 0,117x. Подставим соответствующие значения x в уравнение и найдем новые значения ŷ_x:

ŷ_x = 2,248 + 0,117 • 1 = 2,365;

ŷ_x = 2,248 + 0,117 • 7 = 3,067 и т.п.

Параметры уравнения а₀ и а₁ можно определить и по следующим формулам:

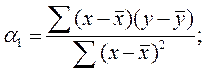
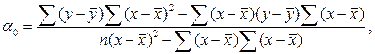
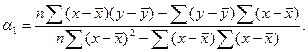
Изобразим по найденным значениям ŷ_x теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 11.2.).

Так как 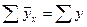, то можно считать, что построенное парное уравнение корреляции является искомым, и, следовательно, сделать следующий вывод: с увеличением стажа работы на один год разряд рабочих в среднем возрастает на 0,117.

Как было сказано ранее, экономическая интерпретация аналитического уравнения связи может осуществляться с помощью коэффициента эластичности. Расчетное значение коэффициента эластичности:

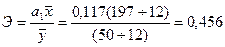
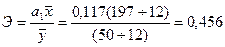
Таким образом, увеличение стажа работы на 1% приводит к увеличению разряда на 0,456%.

Ранее говорилось, что для установления тесноты связи между факторным и результативным признаками в случае линейной зависимости применяется линейный коэффициент корреляции. Рассчитаем его величину:

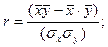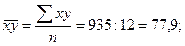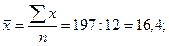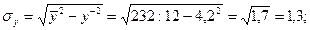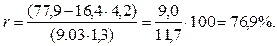Следовательно, на 76,9% разряд рабочего определяется стажем работы на предприятии.

Можно определять r и по другим формулам:

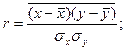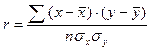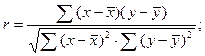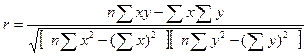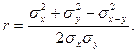Анализ взаимосвязи между явлениями можно также проводить по сгруппированным данным, представленным в виде корреляционной таблицы. Приведем пример корреляционной таблицы, характеризующей связь между стажем рабочих и их заработной платой (талб. 25).

Таблица 25

Стаж работы, Лет (х)	Заработная плата, тыс. руб.	Итого
40-50	50-60	60-70	70-80	80-90	90-100	100-110
0-5 5-10 10-15 15-20 20-25 25-30	- - - - -	- - - -	- - -	- -	-	- -	- -
Итого ny

Корреляционная таблица показывает, что частоты (численность) рабочих концентрируются главным образом у диагонали. Это значит, что связь между стажем рабочего и его заработной платой прямая, т.е. с увеличением стажа заработная плата рабочего

возрастает. Характер линейной зависимости более четко прослеживается на графике (рис.11.3). Для построения эмпирической линии регрессии рассчитаны средние показатели заработной платы по каждой из шести групп рабочих, выделенных по стажу работы:

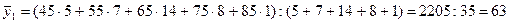
Прямолинейность зависимости заработной платы рабочих от стажа работы на предприятии хорошо видна на рис.11.3. Такую зависимость можно выразить уравнением прямой:

ŷ_x = α₀ + α₁x.

Для построения уравнения зависимости, т.е. нахождения его параметров α₀ и α₁, необходимо решить систему нормальных уравнений с использованием метода наименьших квадратов:

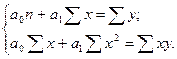
Для этого построим вспомогательную таблицу для x (табл. 26).

Таблица 26

Х	2,5	7,5	12,5	17,4	22,5	27,5	Итого
nx
xnx	87,5	187,5	212,5	192,5	157,5	137,5
x2nx	218,7	1406,3	2656,3	3368,8	3543,8	3781,3	14975,2

В табл. 11.6. в качестве х берутся его средние значения в интервалах группировки: х₁=(0+5):2=2,5; х₂=(5+10):2=7,5; ми т.д. Умножая найденные групповые средние х на численность каждой группы n_x, получим xn_x в пределах данной группы. Суммируя полученные величины по группам, получим общую 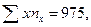которая, и будет выступать в качестве 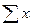в решении системы уравнений.

Суммируя величины x²n, по группам, получим общую 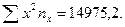Эта суммарная величина будет выступать в качестве 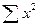для решения системы уравнений.

Построим вспомогательную таблицу для у (табл. 11.7.), взяв в качестве у его среднее значение в интервалах группировки, а именно: 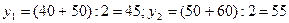и т.д. Умножая найденные групповые средние у на численность каждой группы n_y, получим yn_y в пределах данной группы. Суммируя полученные величины по группам,

получим общую 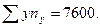Эта суммарная величина, и будет выступать в качестве 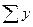в решении системы уравнений.

Таблица 27.

Y								Итого
ny
yny
Y2ny
nxy	562,5			14812,5		29212,5	7612,5

Несколько сложнее с 2. Но если интервалы группировки малы, то можно считать значения у для всех единиц в рамках группы одинаковыми. Умножив средние значения х в интервалах группировки на соответствующие средние значения у и на численность данной группы, получим nxy в пределах данной группы. Так, по данным табл. 24, 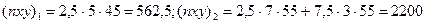и т.д. Сумма полученных значений по группам дает общую величину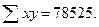

Подставим найденные значения в систему уравнений и решим ее:

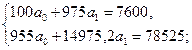
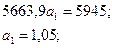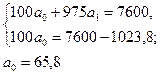Следовательно, аналитическое уравнение связи заработной платы рабочих и стажа их работы имеет вид: 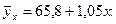На основе данного уравнения можно сделать вывод: с увеличением стажа работы на 1 год заработная плат рабочего увеличивается на 1,05 тыс. руб.

Рассчитаем тесноту связи между х и у с помощью линейного коэффициента корреляции:

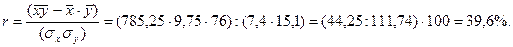
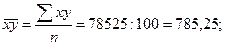
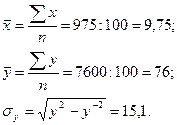
Таким образом, заработная плата на 39,6% зависит от стажа работы на предприятии.

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза (Н₀) о равенстве коэффициента корреляции нулю 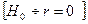. При проверке этой гипотезы используется t-статистика:

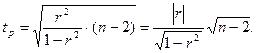
При выполнении Н₀ t-статистика имеет распределение Стьюдента с входными параметрами

Если расчетное значение 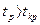(табличное), то гипотеза Н₀ отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а, следовательно, и о существенной зависимости между х и у.

Данный критерий проверяется для совокупности n<50; еслиn>100, то используется формула t-статистики:

Если связь криволинейная, то определяется не линейный коэффициент корреляции, а индекс корреляции:

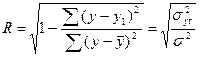, где

y_t- теоретическое значение признака;

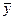- среднее фактическое значение признака.

В случае наличия линейной и нелинейной зависимости между двумя признаками, для измерения тесноты связи применяют корреляционное отношение. Различают эмпирическое и теоретическое корреляционной отношение.

Эмпирическое корреляционное отношение:

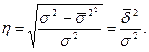
Теоретическое корреляционное отношение:

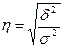, где

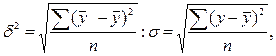тогда

В основе расчета лежит правило сложения дисперсий, о котором говорилось в предыдущей разделе.

Общая формула корреляционного отношения:

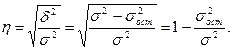
Данный показатель характеризует отклонения групповых средних результативного показателя от общей средней и изменяется в пределах от 0 до 1.

Методы изучения и измерения тесноты связи, приведенные выше, очень сложны. Но в статистике имеются и более простые методы определения тесноты связи: коэффициент корреляции знаков, ранговые коэффициенты Спирмена и Кендалла. Рассмотрим коэффициент корреляции знаков:

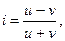где

u – число пар с одинаковыми знаками отклонений х и у от 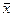и ;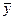

v – число пар с разными знаками отклонений х и у от 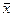и .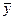

Пример:

Таблица 28

№ завода	Основные фонды (х)	Выпуск продукции	Отклонения
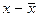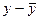		2,4 4,0 3,6 4,0 4,5 4,6 5,6 6,5 7,0 5,0	- - - - - + + + + +	- - - - - - + + + +

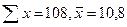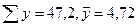u=9, v=1, тогда 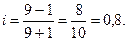Связь – высокая.

Если нужно определить и измерить связь качественных признаков, то можно использовать коэффициенты ассоциации и контингенции.

Коэффициент ассоциации:

Коэффициент контингенции:

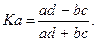
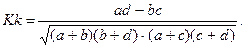
Коэффициент контингенции меньше коэффициента ассоциации. Связь считается подтвержденной, если К_а>0,5 или К_к>0,3.

Пример:

Таблица 29

Семейное положение	Имеют отдельную квартиру	Не имеют отдельной квартиры	Всего
Семейные Одинокие	300 (а) 15 (с)	115 (b) 70 (d)	415 (a+b) 85 (c+d)
Всего	315 (а+с)	185 (b+d)

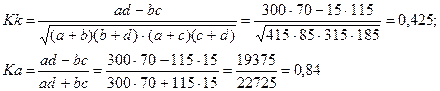
Значения полученных коэффициентов выше нормативных. Значит, оба фактора действительно взаимосвязаны.