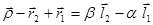 .
.
Умножая скалярно это равенство на 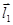 и
и 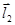 , получим систему уравнений для нахождение величин
, получим систему уравнений для нахождение величин 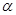 и
и 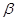 :
:
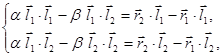
.
что позволяет найти расстояние между прямыми и координаты точек пересечения прямых с их общим перпендикуляром
Если 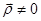 , то прямые скрещиваются (направляющие векторы неколлинеарны) или параллельны (направляющие векторы коллинеарны). Если
, то прямые скрещиваются (направляющие векторы неколлинеарны) или параллельны (направляющие векторы коллинеарны). Если 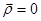 , то
, то 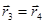 , при
, при
этом прямые пересекаются (направляющие векторы неколлинеарны) или совпадают (направляющие векторы коллинеарны).
Расстояние между прямыми с неколлинеарными направляющими векторами можно определить через разность проекций векторов 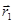 и
и 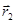 на направление общей нормали
на направление общей нормали
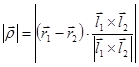 .
.
II. Пусть плоскости заданы нормальными векторами 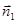 и
и 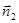 и радиус-векторами фиксированных точек
и радиус-векторами фиксированных точек 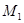 и
и 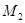 в этих плоскостях
в этих плоскостях 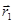 и
и 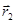 . Если векторы
. Если векторы 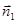 и
и 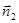 коллинеарны, то плоскости совпадают или параллельны. В этом случае, аналогично предыдущему, расстояние между плоскостями можно определить через разность проекций векторов
коллинеарны, то плоскости совпадают или параллельны. В этом случае, аналогично предыдущему, расстояние между плоскостями можно определить через разность проекций векторов 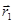 и
и 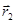 на направление общей нормали
на направление общей нормали
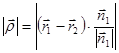 .
.
III. Информация о нормальных и направляющих векторах позволяет определять:
1) угол между двумя плоскостями 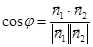 ,
,
2) угол между плоскостью и прямой 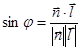 ,
,
3) 3) угол между двумя прямыми 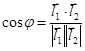 .
.
 2014-02-12
2014-02-12 456
456








