Прямая линия на плоскости

Пример 9.

В тетраэдре, заданном в примере 7, определить угол .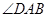

Для определения угла между прямыми необходимо знать их направляющие векторы. Вектор 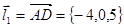вычислялся в предыдущем примере, а вектор 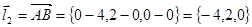. Искомый угол

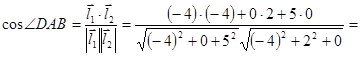
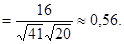
Окончательно .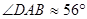

Частным случаем расположения прямой является прямая линия на плоскости. Ее уравнение можно получить как линию пересечения произвольно расположенной плоскости 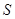и плоскости .

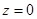Тогда из общего уравнения плоскости находим

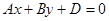- общее уравнение прямой линии на плоскости,

а из уравнения плоскости в отрезках

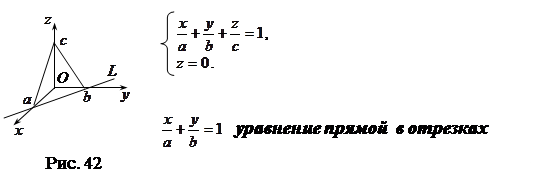Прямая 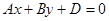делит плоскость на две полуплоскост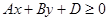и и .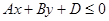

Уравнение прямой на плоскости можно получить как проекцию пространственной прямой, заданной уравнением

,

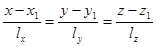на плоскость .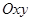

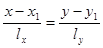- уравнения прямой в канонической форме,

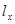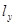где и - координаты двумерного направляющего вектора.

Если направляющий вектор задан координатами точек его начала и конца

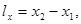
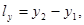
то

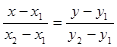- уравнения прямой, проходящей через две точки

Это уравнение приводится к виду

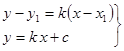- уравнения прямой сугловымкоэффициентом,

где 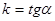, 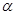- угол между осью 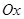и прямой, отсчитываемый против хода часовой стрелки; 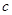- координата пересечения прямой с осью .

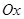Информация об угле наклона прямой к оси 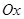позволяет решать следующие задачи:

1) определение угла 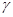между прямым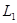и и 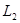, заданными

уравнениями с угловыми коэффициентам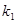и и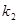

;

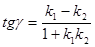2) нахождение прямой 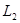, перпендикулярной 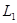и проходящей через заданную точку .

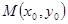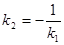тогда : ;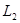

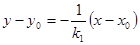3) нахождение прямой 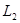, параллельной 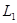и проходящей через заданную точку .

: .

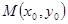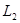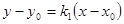Уравнение прямой линии 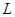можно получить из условия перпендикулярности двухмерного нормального вектора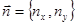, проведенного из начала координат к прямой и вектора 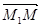, соединяющего фиксированную и произвольную точки прямо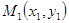й и .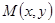

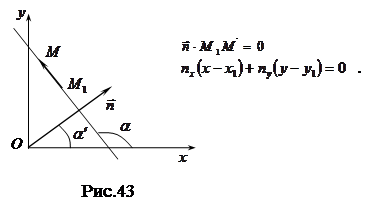Если вектор 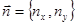задан модулем и направляющими косинусами

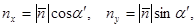
то

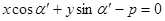- нормальное уравнение прямой линии,

где 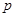- расстояние от начала координат до прямой, 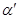- угол между вектором нормали, проведенным из начала координат к прямой, и осью 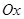. Отклонение точки 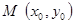от прямой линии находится по формуле

,

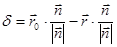или .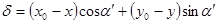

При 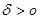точка 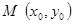и начало координат лежат по разную сторону от прямой.