2014-02-12
2276
Установить взаимное расположение прямых:
; 
.
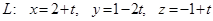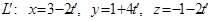Система относительно параметров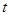 
и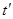 
имеет вид:
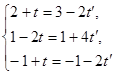или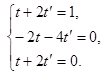 
Вычислим ранг расширенной матрицы:
.
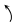
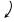
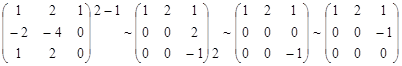Ранг расширенной матрицы равен двум, а основной единице. Система несовместна, прямые параллельны, т.к. направляющие векторы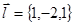 
и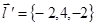 
коллинеарны.
Для определения расстояния между прямым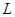и 
и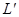 
запишем уравнение плоскости 
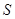, проходящей через точку 
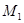пересечения прямой 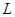с плоскостью 
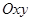и имеющей нормальный вектор 
.
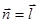Из уравнений прямой 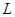следует: при 
.
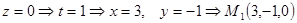Тогда :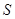 
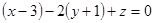. Определим точку 
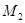пересечения этой плоскости с прямой 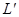, подставляя в это уравнение координаты 
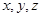из уравнений прямой .
.
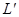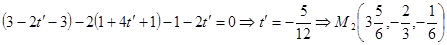Искомое расстояние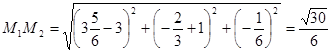 
.
II. Плоскости могут быть параллельными и пересекающимися.
Если плоскости заданы общими уравнениями:
,
,
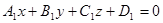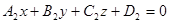то, объединив их в систему, можно решить вопрос о её совместности.
Если система совместна (ранги расширенной и основной матриц равны), то плоскости пересекаются (нормальные векторы не коллинеарны) или совпадают (нормальные векторы коллинеарны). Если система не имеет решений (ранги расширенной и основной матриц не равны), то плоскости параллельны.
III. Прямая может лежать в плоскости, пересекать плоскость или быть параллельной ей. Пусть плоскость задана общим уравнением, а прямая уравнениями в параметрической форме:
.
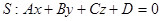
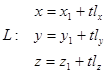
Объединим эти уравнения в систему четырёх уравнений с четырьмя неизвестными (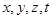
).
Если система несовместна, то прямая и плоскость не имеют общих точек, т.е. они параллельны. Если решение единственно, то оно даёт координаты точки пересечения. Если система неопределённая (бесконечно много решений), то прямая лежит в плоскости. Учитывая вид этой системы, можно упростить вычисления, если подставить 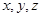из параметрических уравнений прямой в уравнение плоскости. При решении полученного уравнения возможны три случая. Решение единственно – прямая пересекает плоскость. Решений бесконечно много – прямая лежит в плоскости. Решений нет – прямая параллельна плоскости.
