Уравнение регулятора

ЛЕКЦИЯ №11

Центробежный регулятор (центробежный маятник)

Рассмотрим силы, действующие на муфту регулятора скорости. К муфте приложены две приведенные силы:

1) упругая или поддерживающая сила ;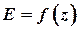

2) регулирующая (приведенная центробежная)сила .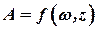

Изобразим зависимост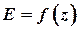и и .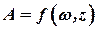

При установившемся движении, которому соответствует координата z ₀ (точка А на рисунке 11.1), регулятор находится в равновесии:

.

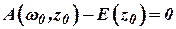(11.1)

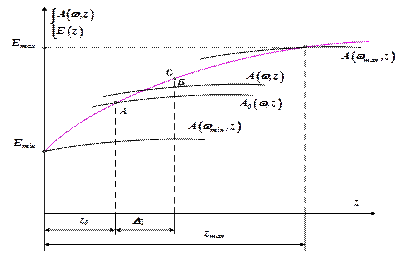
Рисунок 11.1 – Силы действующие на муфту регулятора скорости

Предположим, мы имеем дело с малым возмущением силового поля, а следовательно, с малыми колебаниями муфты около положения равновесия:

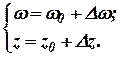Обозначим массу, приведенную к муфте, через М, тогда движение регулятора описывается дифференциальным уравнением

,

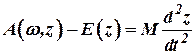(11.2)

Далее обозначим:

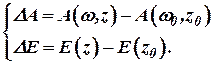
Вычтем (11.1) из (11.2), получим уравнение малых колебаний регулятора

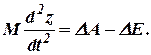
Так как

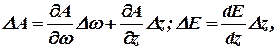
то уравнение регулятора принимает вид:

.

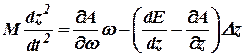(11.3)

Для улучшения процесса регулирования в некоторых схемах вводят демпферы, называемыми катарактами (рис. 11.2), у которых степень демпфирования изменяются с помощью дросселя (перекрытие канала 3).

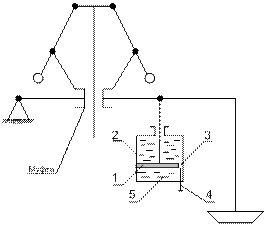
Рисунок 11.2 – Катаракт:

1 – поршень; 2 – цилиндр; 3 – зазор; 4 – дроссель; 5 – масло.

Вследствие действия катаракты на муфту регулятора, возникает сила демпфирования:

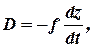
где 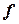– коэффициент пропорциональности, учитывающий передаточное число от приложения силы катаракта к муфте. Знак минус указывает, что сила катаракты всегда направлена в сторону, противоположную движению муфты. С учетом силы 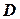уравнение регулятора примет вид:

.

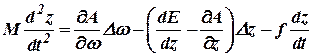(11.4)

Введем относительные переменные:

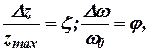
где 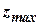– максимальный рабочий ход муфты, соответствующий максимальному статическому изменению регулируемой величины;

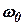– значение регулируемой величины при режиме, который подвергается исследованию.

Тогда (11.4) примет вид:

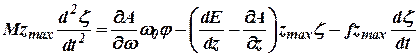(11.4)

или

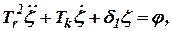(11.5)

где

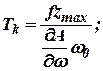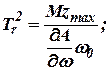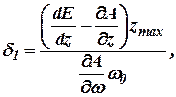где 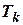– время катаракты;

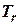– время регулятора.

Если нет катаракты, т.е. демпфирование отсутствует, то уравнение регулятора из-за 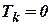с учетом постоянной скорости вращения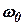 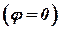станет таким:

.

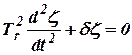(11.6)

Такое уравнение описывает гармонические колебание.

Для увеличения быстродействия регулятора необходимо увеличивать частоту собственных колебаний, т.е. чтобы можно было пренебречь его массой. А это требует 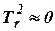, что достигается путем проектирования регулятора с малой приведенной массой и большой поддерживающей (силой упругости) силы.