Теорема: Для того, чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости.
([AB] [BC])
[BC])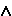 ([AB]
([AB]
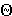 ,[BC]
,[BC]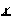
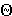 )
)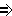 [A
[A B
B ]
] [B
[B C
C ]
]
 Рис.6
Рис.6
| Дано:  ABC=90 ABC=90 [AB] [AB] 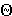 Доказать: Доказать: 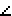 A A B B C C =90 =90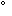
|
Спроецируем [AB] и [BC] на плоскость 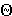 .
.
[AB] [A
[A B
B ]
]
[BC] [B
[B C
C ]
]
Фигура ABB A
A - прямоугольник, следовательно [AB]
- прямоугольник, следовательно [AB] плоскости BCC
плоскости BCC B
B , так как он перпендикулярен двум пересекающимся прямым этой плоскости (AB
, так как он перпендикулярен двум пересекающимся прямым этой плоскости (AB BC по условию и AB
BC по условию и AB BB
BB по построению).
по построению).
Но AB A
A B
B , следовательно A
, следовательно A B
B A
A B
B плоскости BCC
плоскости BCC B
B , поэтому A
, поэтому A B
B
 B
B C
C ,
,
т.е.  A
A B
B C
C =90
=90 .
.
Обратное утверждение также верно.
По Гордону:
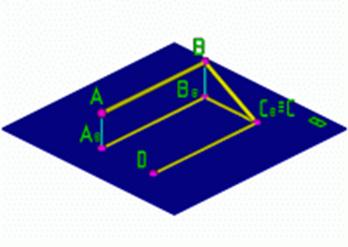 Рис.7
Рис.7
| Дано:  ABC=90 ABC=90 [AB] [AB]  Доказать: Доказать: 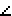 A A B B C C =90 =90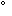
|
Пусть [BC]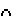
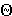 =C
=C
Спроецируем [AB] и [BC] на плоскость 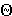 .
.
[AB]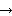 [A
[A B
B ]
]
[BC]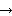 [B
[B C
C ]
]
Проведём [DC] [A
[A B
B ]
]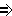 [DC]
[DC] [AB], поэтому
[AB], поэтому 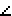 BCD=90
BCD=90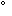
На основании теоремы о 3-х перпендикулярах: (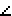 B
B CD=90
CD=90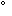 )
)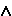 (
(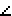 BCD=90
BCD=90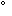 )
)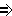
 A
A B
B C=90
C=90 .
.
Верно также обратное утверждение. Эту теорему применяют при решении задач на определение расстояния от точки до прямой частного положения.
Пример:
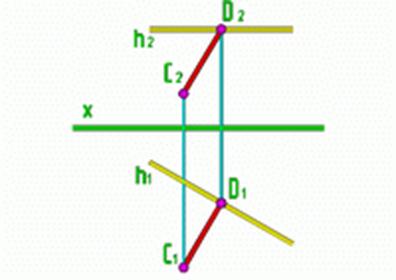 Рис.8
Рис.8
| Дана горизонталь h и точка С. Надо опустить перпендикуляр из точки C на прямую h. Перпендикуляр из точки C к прямой h образует угол 90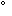 и h и h H, следовательно прямой угол без искажения проецируется на плоскость H, поэтому из горизонтальной проекции точки C надо опустить перпендикуляр к h1 (горизонтальной проекции горизонтали). |C1D1|=|CD| H, следовательно прямой угол без искажения проецируется на плоскость H, поэтому из горизонтальной проекции точки C надо опустить перпендикуляр к h1 (горизонтальной проекции горизонтали). |C1D1|=|CD|
|
 2014-02-12
2014-02-12 554
554








