Плоскость - простейшая поверхность (1-го порядка).
1. Плоскость, её задание на чертеже.
Положение плоскости в пространстве может быть задано:
- Тремя точками, не лежащими на одной прямой.
- Прямой и точкой вне прямой.
- Двумя прямыми, пересекающимися в несобственной точке (пересекающимися или параллельными).
Соответственно и на чертеже (эпюре) плоскость может быть задана аналогично.
Задание плоскости на чертеже производится проекциями этих же геометрических элементов. Кроме того, плоскость может быть задана также проекциями отсека плоской фигуры (Ф).
Иногда целесообразно задать плоскость не произвольными пересекающимися прямыми, а прямыми, по которым эта плоскость пересекает плоскости проекций. Эти прямые называют следами плоскости, а такой вариант задания плоскости называют методом задания плоскости следами.
Примеры задания плоскости:
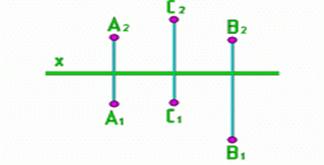 Рис.9
Рис.9
| Тремя точками |
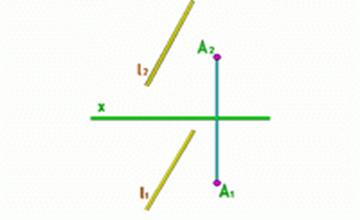 Рис.10
Рис.10
| Точкой и прямой |
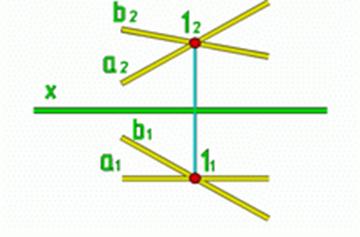 Рис.11
Рис.11
| Пересекающимися прямыми |
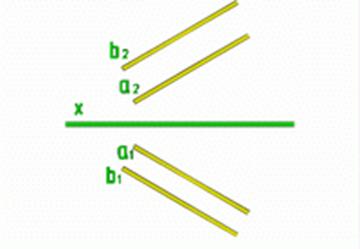 Рис.12
Рис.12
| Параллельными прямыми |
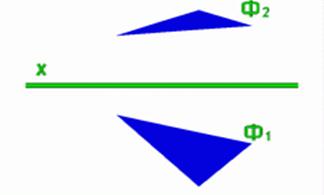 Рис.13
Рис.13
| Отсеком плоскости |
 2014-02-12
2014-02-12 553
553








