Центральные проекции. Предположим, что центр проекции находится в точке , а картинная плоскость совпадает с плоскостью

Предположим, что центр проекции находится в точке 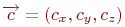, а картинная плоскость совпадает с плоскостью . Возьмем произвольную точку изображаемого объекта 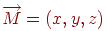и определим ее проекцию на выбранную плоскость (рис. 7.7).

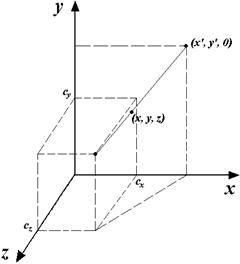
Рис. 7.7. Центральная проекция на плоскость XOY

Прямую, проходящую через точк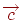и и 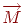, зададим в параметрическом виде:

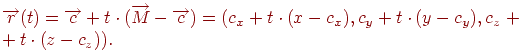
(7.1)

Теперь найдем точку пересечения этой прямой с картинной плоскостью. Она определяется из условия равенства нулю третьей координаты:

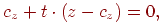
откуда определяем значение параметра 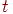, при котором точка прямой принадлежит координатной плоскости:

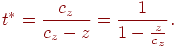
Подставляя это значение в формулу (7.1), мы получим координаты проекции точки :

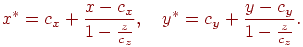
(7.2)

Фактором, влияющим на перспективное изменение размеров, является наличие координаты 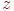в знаменателе. Чем ближе оказывается точка к центру проекции, тем больше знаменатель, а соответственно и координаты точки.

Мы будем рассматривать ситуацию, когда центр проекции лежит на оси 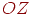, а сама ось направлена от наблюдателя к проекционной плоскости, т.е. 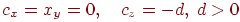. Тогда формулы (7.2) приобретают вид

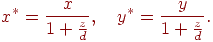
(7.3)

В однородных координатах такое преобразование можно записать с помощью двух операций. Сначала умножаем матрицу проективного преобразования 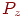на исходную точку и получаем точку в четырехмерном пространстве:

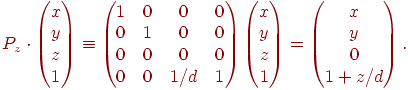
(7.4)

Затем проецируем эту точку в пространство однородных координат путем деления на четвертую компоненту:

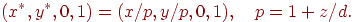
Посмотрим теперь, что происходит с пучком параллельных прямых под действием матрицы проекции. Пусть задан пучок прямых, параллельных вектору 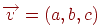. Тогда параметрическое уравнение прямой, принадлежащей этому пучку, имеет вид

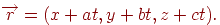
Из формулы (7.4) следует, что в результате проецирования получим множество точек

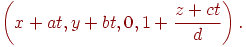
Переходя к однородным координатам и умножив числитель и знаменатель каждой дроби на 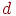, получим точки 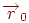вида

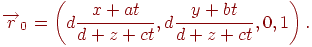
Теперь в каждой компоненте вектора числитель и знаменатель поделим на :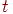

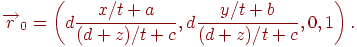
Переходя к пределу при 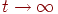, получим точку

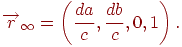
Таким образом, получаем, что после проецирования пучок параллельных прямых пересекается в точке схода 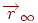. Понятно, что у каждого пучка своя точка схода. Если пучок прямых параллелен плоскости , т.е. , то точка схода оказывается на бесконечности, а значит, прямые остаются параллельными.

Для построения перспективной проекции с несколькими точками схода используется матрица перспективного преобразования без проецирования:

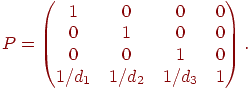
Теперь точки пространства сначала подвергаются перспективному преобразованию, а затем осуществляется проекция.

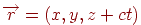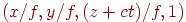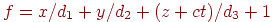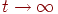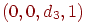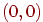Определим точки схода для прямых, параллельных осям координат. Для прямых результатом проективного преобразования будет множество точек , где . При получим точку с координатами . При проекции на плоскость получим точку . Пучок прямых 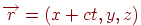перейдет в 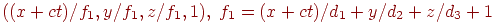, а точкой схода для него будет 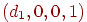, которая при проецировании перейдет в точку, лежащую на оси 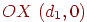. Аналогично для пучка прямых, параллельных оси 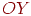, получим точку схода на оси 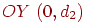. Эти три точки на плоскости являются главными точками схода.