Пусть Х ~ N (m, σ2) причем 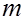 и
и 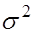 - неизвестны. Пусть для оценки
- неизвестны. Пусть для оценки 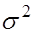 извлечена выборка объема
извлечена выборка объема 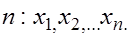
1. В качестве точечной оценки дисперсии 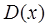 используется исправленная выборочная дисперсия:
используется исправленная выборочная дисперсия: 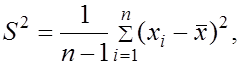 которой соответствует стандартное отклонение
которой соответствует стандартное отклонение 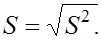
2. При нахождении доверительного интервала для дисперсии в этом случае вводится статистика 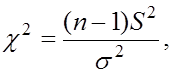 имеющая
имеющая 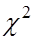 - распределение с числом степеней свободы
- распределение с числом степеней свободы 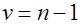 независимо от значения параметра
независимо от значения параметра 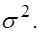
3. Задается требуемый уровень значимости 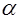 .
.
4. Тогда, используя таблицу критических точек 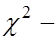 распределения, нетрудно указать критические точки
распределения, нетрудно указать критические точки 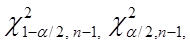 для которых будет выполняться следующее равенство:
для которых будет выполняться следующее равенство:
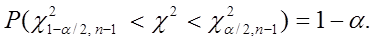 (32)
(32)
Неравенство 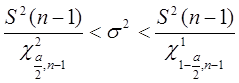 (33)
(33)
может быть преобразовано в следующее:
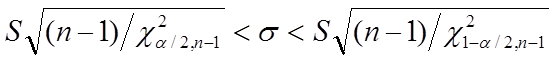 (34)
(34)
Таким образом, доверительный интервал 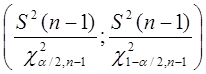 накрывает неизвестный параметр
накрывает неизвестный параметр 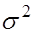
 с надежностью
с надежностью 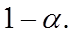 А доверительный интервал
А доверительный интервал 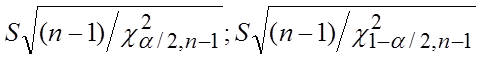 с надежностью
с надежностью 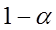 накрывает неизвестный параметр
накрывает неизвестный параметр 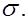
 2014-02-09
2014-02-09 1051
1051








