На начальном этапе в качестве оценки той или иной числовой характеристики (математического ожидания, дисперсии и т.п.) берется выборочная числовая характеристика. Затем, исследуя эту оценку, ее уточняют таким образом, чтобы она удовлетворяла описанным выше свойствам.
Доказано, что выборочное среднее 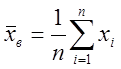 является несмещенной и состоятельной оценкой математического ожидания M(X) генеральной совокупности.
является несмещенной и состоятельной оценкой математического ожидания M(X) генеральной совокупности.
Выборочная дисперсия 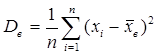 является смещенной, но состоятельной оценкой дисперсии
является смещенной, но состоятельной оценкой дисперсии 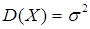 СВ Х генеральной совокупности, т.к. доказано, что
СВ Х генеральной совокупности, т.к. доказано, что 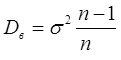
Иными словами, выборочная дисперсия оценивает генеральную дисперсию с недостатком.
Хотя при 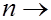 ∞
∞ 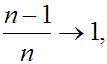 и оценка
и оценка 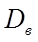 является асимптотически несмещенной, в качестве оценки дисперсии
является асимптотически несмещенной, в качестве оценки дисперсии 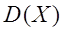 удобнее брать исправленную дисперсию:
удобнее брать исправленную дисперсию:
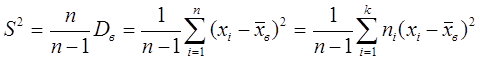 (24)
(24)
Исправленная дисперсия 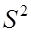 является несмещенной и состоятельной оценкой дисперсии
является несмещенной и состоятельной оценкой дисперсии 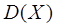 СВ
СВ 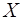 .
.
Аналогично вводится исправленное среднее квадратическое отклонение или так называемый эмпирический стандарт 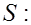
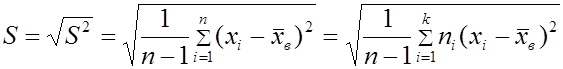 (25)
(25)
Отметим, что при 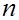 >30 различие между
>30 различие между 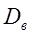 и
и 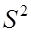
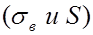 практически незначимо. Поэтому при большом объеме выборки и ту, и другую оценки можно считать несмещенными.
практически незначимо. Поэтому при большом объеме выборки и ту, и другую оценки можно считать несмещенными.
Относительная частота 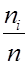 является несмещенной и состоятельной оценкой вероятности
является несмещенной и состоятельной оценкой вероятности 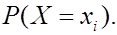 Аналогично эмпирическая функция распределения
Аналогично эмпирическая функция распределения 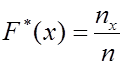 (накопленная относительная частота) является несмещенной и состоятельной оценкой (теоретической) функции распределения
(накопленная относительная частота) является несмещенной и состоятельной оценкой (теоретической) функции распределения 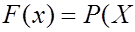 <
< 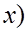 .
.
После получения точечной оценки 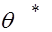 , желательно иметь данные о надежности такой оценки. Особенно важно иметь сведения о точности оценок для небольших выборок (поскольку с возрастанием объема
, желательно иметь данные о надежности такой оценки. Особенно важно иметь сведения о точности оценок для небольших выборок (поскольку с возрастанием объема 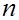 выборки несмещенность и состоятельность основных оценок гарантируется утверждениями математической статистики).
выборки несмещенность и состоятельность основных оценок гарантируется утверждениями математической статистики).
Точечная оценка может быть дополнена интервальной оценкой – интервалом 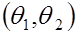 , внутри которого с наперед заданной вероятностью
, внутри которого с наперед заданной вероятностью 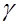 находится точное значение оцениваемого параметра
находится точное значение оцениваемого параметра 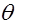 . Определение такого интервала называют интервальным оцениванием, а сам интервал – доверительным интервалом. При этом
. Определение такого интервала называют интервальным оцениванием, а сам интервал – доверительным интервалом. При этом 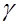 называют доверительной вероятностью – или надежностью, с которой оцениваемый параметр
называют доверительной вероятностью – или надежностью, с которой оцениваемый параметр 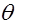 попадает в интервал
попадает в интервал 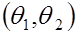 .
.
Для определения доверительного интервала заранее выбирают число 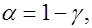
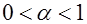 , называемое уровнем значимости, и находят два числа
, называемое уровнем значимости, и находят два числа 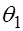 и
и 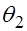 , зависящих от точечной оценки
, зависящих от точечной оценки 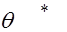 , такие, что
, такие, что
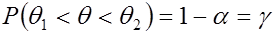 (26)
(26)
В этом случае говорят, что интервал 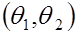 накрывает неизвестный параметр
накрывает неизвестный параметр 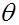 с вероятностью
с вероятностью 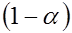 . Границы интервала
. Границы интервала 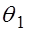 и
и 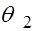 называются доверительными, и они обычно находятся из условия
называются доверительными, и они обычно находятся из условия 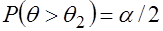
Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки 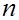 и надежности
и надежности 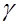 (уровня значимости
(уровня значимости 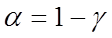 ). При увеличении величины
). При увеличении величины 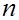 длина доверительного интервала уменьшается, а с приближением надежности
длина доверительного интервала уменьшается, а с приближением надежности 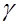 к единице – увеличивается. Выбор
к единице – увеличивается. Выбор 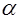 (или
(или 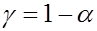 ) определяется конкретными условиями. Обычно используется
) определяется конкретными условиями. Обычно используется 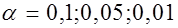 , что соответствует 90, 95, 99%-м доверительным интервалам.
, что соответствует 90, 95, 99%-м доверительным интервалам.
Общая схема построения доверительного интервала:
1. Из генеральной совокупности с известным распределением 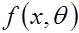
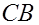
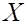 извлекается выборка объема
извлекается выборка объема 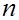 , по которой находится точечная оценка
, по которой находится точечная оценка 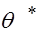 параметра
параметра 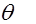 .
.
2. Строится 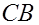
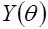 , связанная с параметром
, связанная с параметром 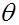 и имеющая известную плотность вероятности
и имеющая известную плотность вероятности 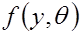 .
.
3. Задается уровень значимости 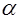 .
.
4. Используя плотность вероятности 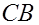
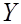 , определяют два числа
, определяют два числа 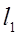 и
и 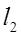 такие, что
такие, что 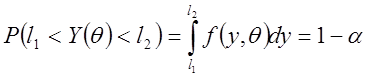 (27)
(27)
5. Выбираются значения 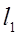 и
и 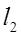 из условий
из условий
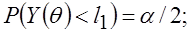
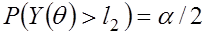 .
.
Неравенство 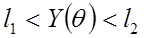 преобразуется в равносильное
преобразуется в равносильное 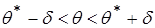 такое, что
такое, что 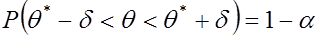 (28)
(28)
Полученный интервал 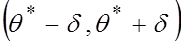 , накрывающий неизвестный параметр
, накрывающий неизвестный параметр 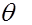 с вероятностью
с вероятностью 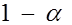 , и является интервальной оценкой параметра
, и является интервальной оценкой параметра 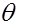 .
.
Интервальная оценка также носит случайный характер, т.к. она напрямую связана с результатами выборки. Она позволяет сделать следующий вывод.
Если построен доверительный интервал, который с надежностью 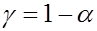 накрывает неизвестный параметр, и его границы рассчитываются по
накрывает неизвестный параметр, и его границы рассчитываются по 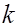 выборкам одинакового объема
выборкам одинакового объема 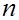 , то в
, то в 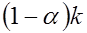 случаях построенные интервалы накрывают истинное значение исследуемого параметра.
случаях построенные интервалы накрывают истинное значение исследуемого параметра.
Поскольку в эконометрических задачах часто приходится находить доверительные интервалы параметров случайных величин, имеющих нормальное распределение, приведем схемы их определения.
I. Доверительный интервал для математического ожидания нормальной 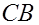 при известной дисперсии
при известной дисперсии
Пусть количественный признак 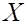 генеральной совокупности имеет нормальное распределение с заданной дисперсией
генеральной совокупности имеет нормальное распределение с заданной дисперсией 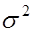 и неизвестным математическим ожиданием m (X ~ N (m, σ2)).
и неизвестным математическим ожиданием m (X ~ N (m, σ2)).
Построим доверительный интервал для 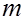 .
.
1. Пусть для оценки 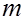 извлечена выборка
извлечена выборка 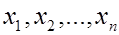 объема
объема 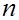 . Тогда
. Тогда 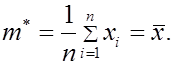
2. Составим СВ 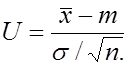 . Нетрудно показать, что СВ
. Нетрудно показать, что СВ 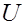 имеет стандартизированное нормальное распределение, т.е.
имеет стандартизированное нормальное распределение, т.е. 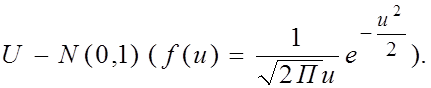
3. Зададим уровень значимости 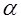 .
.
4. Применяя формулу нахождения вероятности отклонения нормальной величины от математического ожидания, имеем:
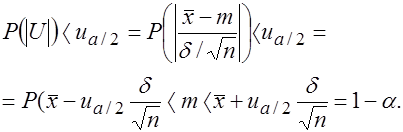 (29)
(29)
Это означает, что доверительный интервал 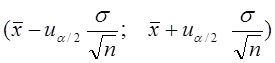 накрывает неизвестный параметр
накрывает неизвестный параметр 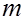 c надежностью
c надежностью 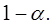 Точность оценки определяется величиной
Точность оценки определяется величиной 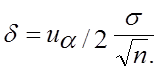
Отметим, что по таблице Лапласа число 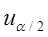 определяется по таблице значений функции Лапласа из равенства
определяется по таблице значений функции Лапласа из равенства 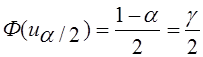 .
.
II. Доверительный интервал для математического ожидания нормальной СВ при неизвестной дисперсии.
В реальной жизни истинное значение дисперсии исследуемой СВ, чаще всего, известно не будет. Это приводит к необходимости использования другой формулы при определении доверительного интервала для математического ожидания СВ, имеющей нормальное распределение.
Для этого из генеральной совокупности СВ 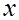 извлекается выборка объема
извлекается выборка объема 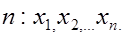
1.В качестве точечной оценки математического ожидания 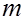 используется выборочное среднее
используется выборочное среднее 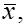 а в качестве оценки дисперсии
а в качестве оценки дисперсии 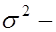 исправленная выборочная дисперсия
исправленная выборочная дисперсия 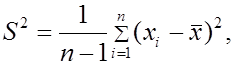 которой соответствует стандартное отклонение
которой соответствует стандартное отклонение 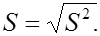
2. Для нахождения доверительного интервала строится статистика 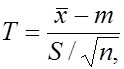 имеющая в этом случае распределение Стьюдента с числом степеней свободы
имеющая в этом случае распределение Стьюдента с числом степеней свободы 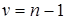 независимо от значений параметров
независимо от значений параметров 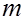 и
и 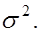
3. Задается требуемый уровень значимости 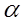 .
.
4. Применяется следующая формула расчета вероятности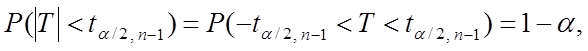 (30)
(30)
где 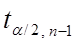 - критическая точка распределения Стьюдента, которая находится по соответствующей таблице.
- критическая точка распределения Стьюдента, которая находится по соответствующей таблице.
Тогда 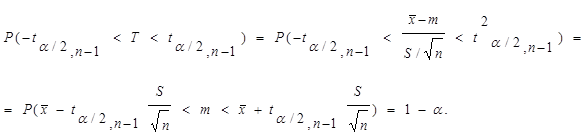
(31)
Это означает, что интервал 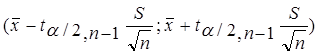 накрывает неизвестный параметр
накрывает неизвестный параметр 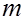 с надежностью
с надежностью 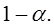
 2014-02-09
2014-02-09 2187
2187
