Статистической гипотезойназывается любое предположение о виде закона распределения или о параметрах неизвестного закона распределения. В первом случае гипотеза называется непараметрической, а во втором параметрической.
Гипотеза 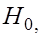 подлежащая проверке, называется нулевой или нуль – гипотезой (основной). Наряду с нулевой рассматривают гипотезу
подлежащая проверке, называется нулевой или нуль – гипотезой (основной). Наряду с нулевой рассматривают гипотезу 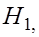 которая будет приниматься, если отклоняется
которая будет приниматься, если отклоняется 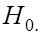 . Такая гипотеза называется альтернативной (конкурирующей).
. Такая гипотеза называется альтернативной (конкурирующей).
Например, если проверяется гипотеза о равенстве параметра 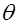 некоторому значению
некоторому значению 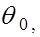 т.е.
т.е. 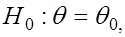 то в качестве альтернативной могут рассматриваться следующие гипотезы:
то в качестве альтернативной могут рассматриваться следующие гипотезы:
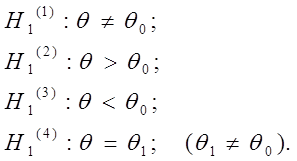
Выбор альтернативной гипотезы определяется конкретной формулировкой задачи, а нулевая гипотеза часто специально подбирается так, чтобы отвергнуть ее и принять тем самым альтернативную гипотезу. Для того, чтобы принять гипотезу о наличии корреляции между двумя экономическими показателями (например, между инфляцией и безработицей), можно опровергнуть гипотезу об отсутствии такой корреляции, взяв ее в качестве нулевой гипотезы.
Гипотезу называют простой, если она содержит одно конкретное предложение 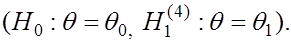
Гипотезу называют сложной, если она состоит из конечного или бесконечного числа простых гипотез: 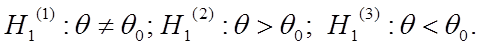

При проверке гипотезы выборочные данные могут противоречить гипотезе  . Тогда она отклоняется. Если же статистические данные согласуются с выдвинутой гипотезой, то она не отклоняется. В последнем случае частот говорят, что нулевая гипотеза принимается. Статистическая проверка гипотез на основании выборочных данных неизбежно связана с риском принятия ложного решения. При этом возможны ошибки двух родов.
. Тогда она отклоняется. Если же статистические данные согласуются с выдвинутой гипотезой, то она не отклоняется. В последнем случае частот говорят, что нулевая гипотеза принимается. Статистическая проверка гипотез на основании выборочных данных неизбежно связана с риском принятия ложного решения. При этом возможны ошибки двух родов.
1. Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза.
2. Ошибка второго рода состоит в том, что будет принята нулевая гипотеза, в то время как в действительности верна альтернативная гипотеза.
Возможные результаты статистических выводов представлены следующей таблицей:
| Результаты проверки гипотезы | Возможные состояния гипотезы | |
верна  | верна  | |
Гипотеза 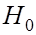 отклоняется отклоняется | Ошибка первого рода, вероятность 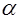 | Правильный вывод, вероятность 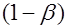 |
Гипотеза 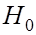 не отклоняется не отклоняется | Правильный вывод, вероятность 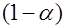 | Ошибка второго рода, вероятность 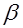 |
Последствия указанных ошибок неравнозначны.
Первая приводит к более осторожному, консервативному решению, вторая – к неоправданному риску.
Исключить вообще ошибки 1–ого и 2–ого рода невозможно в силу ограниченности выборки. Поэтому стремятся минимизировать потери от этих ошибок. Отметим, что одновременное уменьшение вероятностей данных ошибок невозможно, т.к. задачи их уменьшения являются конкурирующими, и снижение вероятности допустить одну из них влечет за собой увеличение вероятности допустить другую. В большинстве случаев единственный способ уменьшения вероятности ошибок состоит в увеличении объема выборки.
Вероятность совершить ошибку 1–ого рода принято обозначать буквой 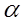 и ее называют уровнем значимости. Вероятность совершить ошибку 2–ого рода обозначают
и ее называют уровнем значимости. Вероятность совершить ошибку 2–ого рода обозначают 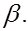 Тогда вероятность не совершить ошибку второго рода
Тогда вероятность не совершить ошибку второго рода 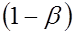 называется мощностью критерия.
называется мощностью критерия.
Обычно значения 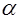 задают заранее, «круглыми» числами (например, 0,1; 0,05; 0,01 и т.п.), а затем стремятся построить критерий наименьшей мощности. Т.о., если
задают заранее, «круглыми» числами (например, 0,1; 0,05; 0,01 и т.п.), а затем стремятся построить критерий наименьшей мощности. Т.о., если 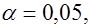 то это означает, что исследователь не хочет совершить ошибку 1–ого рода более чем в 5-ти случаях из 100.
то это означает, что исследователь не хочет совершить ошибку 1–ого рода более чем в 5-ти случаях из 100.
Проверку статистической гипотезы осуществляют на основании данных выборки.Для этого используют специально подобранную СВ (статистику, критерий), точное или приближенное значение которой известно. Эту величину обозначают:
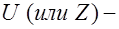 если она имеет стандартизированное нормальное распределение;
если она имеет стандартизированное нормальное распределение;
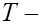 если она распределена по закону Стьюдента;
если она распределена по закону Стьюдента;
χ2 - если она распределена по закону χ2;
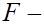 если она имеет распределение Фишера.
если она имеет распределение Фишера.
В целях общности будем обозначать такую СВ через 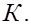
Таким образом, статистическим критерием или статистическим тестом называют СВ 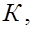 которая служит для проверки нулевой гипотезы. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества:
которая служит для проверки нулевой гипотезы. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества:
- одно из них содержит значения критерия, при которых нулевая гипотеза отклоняется;
- другое – при которых она не отклоняется.
Совокупность значений критерия, при которых нулевую гипотезу отклоняют, называют критической областью.
Совокупность значений критерия, при которых нулевую гипотезу не отклоняют, называют областью принятия гипотезы.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия 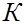 (вычисленное по выборке) принадлежит критической области, то нулевую гипотезу отклоняют. Если же наблюдаемое значение критерия
(вычисленное по выборке) принадлежит критической области, то нулевую гипотезу отклоняют. Если же наблюдаемое значение критерия 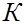 принадлежит области принятия гипотезы, то нулевую гипотезу не отклоняют (принимают).
принадлежит области принятия гипотезы, то нулевую гипотезу не отклоняют (принимают).
Точки, разделяющие критическую область и область принятия гипотезы, называют критическими.
В основу определения критических точек и критической области положен принцип практической невозможности маловероятных событий.
Пусть для проверки нулевой гипотезы 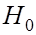 служит критерий
служит критерий 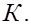 Предположим, что плотность распределения вероятности СВ
Предположим, что плотность распределения вероятности СВ 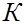 в случае справедливости
в случае справедливости 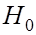 имеет вид
имеет вид 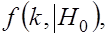 а математическое ожидание
а математическое ожидание 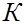 равно
равно 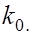
Тогда вероятность того, что СВ 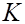 попадет в произвольный интервал
попадет в произвольный интервал 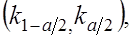 можно найти по формуле:
можно найти по формуле:
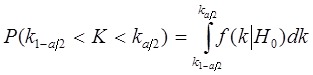 (35)
(35)
Зададим эту вероятность равной 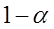 и вычислим критические точки (квантили)
и вычислим критические точки (квантили) 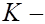 распределения
распределения 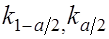 из условий:
из условий:
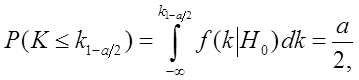 (36)
(36)
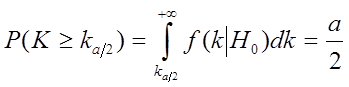 (37)
(37)
Следовательно,
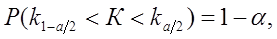
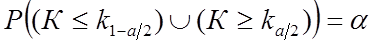 (38)
(38)
Зададим вероятность 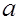 настолько малой (0,05; 0,01), что попадание СВ
настолько малой (0,05; 0,01), что попадание СВ 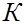 за пределы интервала
за пределы интервала 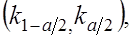 можно было бы считать маловероятным событием. Тогда, исходя из принципа практической невозможности маловероятных событий, можно считать, что если
можно было бы считать маловероятным событием. Тогда, исходя из принципа практической невозможности маловероятных событий, можно считать, что если 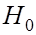 справедлива, то при ее проверке с помощью критерия
справедлива, то при ее проверке с помощью критерия 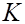 по данным одной выборки наблюдаемое значение
по данным одной выборки наблюдаемое значение 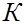 должно наверняка попасть в интервал
должно наверняка попасть в интервал 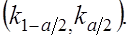
Если же наблюдаемое значение 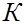 попадает за пределы указанного интервала, то произойдет маловероятное, практически невозможное событие. Это дает основание считать, что с вероятностью
попадает за пределы указанного интервала, то произойдет маловероятное, практически невозможное событие. Это дает основание считать, что с вероятностью 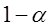 нулевая гипотеза
нулевая гипотеза 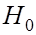 несправедлива.
несправедлива.
Точки 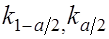 называются критическими.
называются критическими.
Критическая область 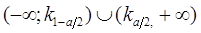 называется двусторонней критической областью. Она определяется в случае, когда альтернативная гипотеза имеет вид
называется двусторонней критической областью. Она определяется в случае, когда альтернативная гипотеза имеет вид 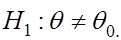
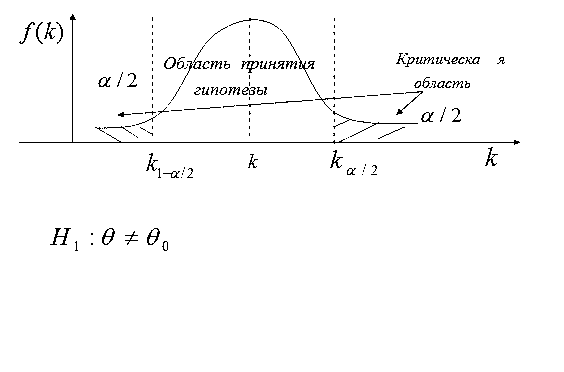
Кроме двусторонней, рассматривают также односторонние критические области – правостороннюю и левостороннюю.
Правосторонней называют критическую область 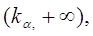 определяющуюся из соотношения
определяющуюся из соотношения 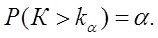
Она используется в случае, когда альтернативная гипотеза имеет вид: 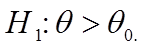
Левосторонней называют критическую область 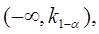 определяющую из соотношения
определяющую из соотношения 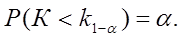
Она используется в случае, когда альтернативная гипотеза имеет вид 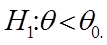
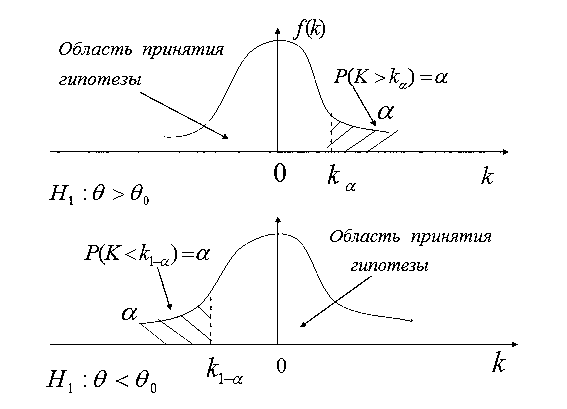
Общая схема проверки гипотез.
1. Формулировка проверяемой (нулевой - 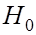 ) и альтернативной
) и альтернативной 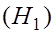 гипотез.
гипотез.
2. Выбор соответствующего уровня значимости α.
3. Определение объема выборки 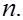
4. Выбор критерия 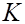 для проверки
для проверки 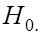
5. Определение критической области и области принятия гипотезы.
6. Вычисление наблюдаемого значения критерия 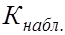
7. Принятие статистического решения.
 2014-02-09
2014-02-09 8252
8252