2014-02-09
396
Выделяют следующие группы нелинейных уравнений регрессии.
Во-первых, это регрессия, нелинейная относительно факторов (объясняющих переменных), но линейная по оцениваемым параметрам. Примерами таких моделей могут быть следующие функции:
· 
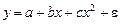– парабола второго порядка;
· 
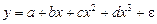– парабола третьего порядка;
· 
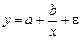– гипербола.
Параметры данных моделей, как и в линейной регрессии, оцениваются обычным МНК, т.к. эти функции линейны по параметрам. Например, в параболе второй степени, заменяя переменные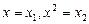 
, получим двухфакторное уравнение регрессии 
.
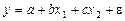К следующей группе относят регрессию, нелинейную по оцениваемым параметрам. В ее составе выделяют две подгруппы.
В одну из них включают нелинейные модели, которые являются внутренне линейными, т.е. те, которые могут быть линеаризованы. Например, степенную функцию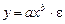 
необходимо прологарифмировать как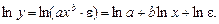 
Для линеаризации обратной модели вида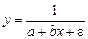 
находится величина, равная 
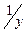. Возможно одновременное использование логарифмирования и нахождения обратных величин (в частности, для логистической функции 
).
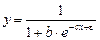Параметры моделей данной подгруппы оцениваются с помощью МНК после их линеаризации, при этом меняется критерий оценки параметров [4]. В частности, он может принять следующий вид:
.
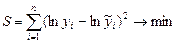Ко второй подгруппе относят модели, которые можно считать внутренне нелинейными. Эти функции не могут быть приведены к линейному виду. Например,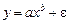 
и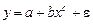 
.
Линеаризация таких моделей невозможна. Поэтому обычный МНК неприменим, а для оценки параметров используются итеративные процедуры, точность которых зависит от конкретного вида уравнений регрессии и от особенностей используемого численного метода.
